题目内容
11.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c为常数a≠0)与x轴,y轴分别交于A,B,C三点,已知A(-1,0),B(3,0),C(0,3),动点E从抛物线的顶点点D出发沿线段DB向终点B运动.(1)求抛物线解析式和顶点D的坐标;
(2)过点E作EF⊥y轴于点F,交抛物线对称轴左侧的部分于点G,交直线BC于点H,过点H作HP⊥x轴于点P,连接PF,求当线段PF最短时G点的坐标;
(3)在点E运动的同时,另一个动点Q从点B出发沿直线x=3向上运动,且速度均为每秒1个单位长度,当点E到达终点B时点Q也随之停止运动,设点E的运动时间为t秒,试问存在几个t值能使△BEQ为等腰三角形?并直接写出相应t值.
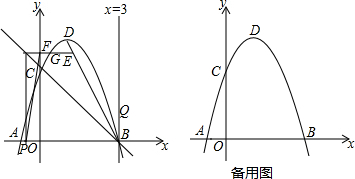
分析 (1)直接把A(-1,0),B(3,0),C(0,3)三点代入抛物线y=ax2+bx+c求得a、b、c得出解析式,进一步求得顶点坐标即可;
(2)连接OH,则四边形HPOF是矩形,利用矩形的性质和垂线段最短求得答案即可;
(3)可用t分别表示出BE、BQ、EQ的长,然后分BE=BQ、BE=EQ、BQ=EQ三种情况,列方程求出t的值.
解答 解:(1)由题意得
$\left\{\begin{array}{l}{0=a-b+c}\\{0=9a+3b+c}\\{3=c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$,
∴抛物线y=-x2+2x+3,
顶点D为(1,4);
(2)如图,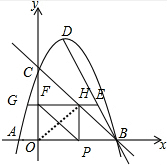
连接OH,
∵EF⊥y轴,HP⊥x轴,x轴⊥y轴,
∴四边形HPOF是矩形,
∴PF=OH,
∴当OH最短时,PF最短,
∴OH⊥BC时,PF最短,
可得H的纵坐标为$\frac{3}{2}$,
把y=$\frac{3}{2}$代入y=-x2+2x+3中,
则$\frac{3}{2}$=-x2+2x+3,
解得x1=$\frac{2-\sqrt{10}}{2}$,x2=$\frac{2+\sqrt{10}}{2}$(舍去);
∴G点的坐标($\frac{2-\sqrt{10}}{2}$,$\frac{3}{2}$);
(3)如图,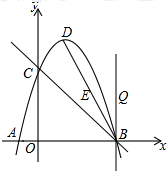
DB=2$\sqrt{5}$,yBD=-2x+6,点E坐标为($\frac{\sqrt{5}t+5}{5}$,$\frac{20-2\sqrt{5}t}{5}$),Q为(3,t),
当BE=BQ时,2$\sqrt{5}$-t=t,t=$\sqrt{5}$;
当BE=EQ时,2$\sqrt{5}$-t=$\sqrt{(\frac{\sqrt{5}t+5}{5}-3)^{2}+(\frac{20-\sqrt{5}t}{5}-t)^{2}}$,t=$\frac{40-10\sqrt{5}}{11}$,
当BQ=EQ时,t=$\sqrt{(\frac{\sqrt{5}t+5}{5}-3)^{2}+(\frac{20-\sqrt{5}t}{5}-t)^{2}}$,t=$\frac{32\sqrt{5}-40}{11}$.
所以存在3个t值,
t1=$\sqrt{5}$,t2=$\frac{40-10\sqrt{5}}{11}$,t3=$\frac{32\sqrt{5}-40}{11}$.
点评 此题考查二次函数综合题,待定系数法求函数解析式,矩形的性质,垂线段最短,平面内两点之间的距离等知识的综合运用,注意分类讨论思想的渗透.

 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案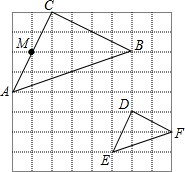 如图,在8×8的正方形网格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上,AC与网格上的直线相交于点M.
如图,在8×8的正方形网格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上,AC与网格上的直线相交于点M. 如图,立方体的六个面上标着连续的自然数.
如图,立方体的六个面上标着连续的自然数.