题目内容
10.圆内接正六边形的边长为10cm,它的边心距等于5$\sqrt{3}$cm.分析 根据题意画出图形,利用等边三角形的性质及锐角三角函数的定义直接计算即可.
解答  解:如图所示,连接OB、OC,过O作OG⊥BC于G,
解:如图所示,连接OB、OC,过O作OG⊥BC于G,
∵此多边形是正六边形,
∴△OBC是等边三角形,
∴∠OBG=30°,
∴边心距OG=OB•sin∠OBG=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$(cm);
故答案为:5$\sqrt{3}$.
点评 本题考查的是正多边形与圆、锐角三角函数的定义及特殊角的三角函数值,熟知正六边形的性质是解答此题的关键.

练习册系列答案
相关题目
2.下列命题中是假命题的是( )
| A. | 所有的矩形是相似的 | |
| B. | 含30°角的直角三角形与含60°角的直角三角形是相似的 | |
| C. | 两个等腰直角三角形是相似的 | |
| D. | 所有的等边三角形都是相似的 |
19.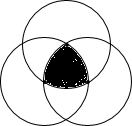 如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )
如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )
 如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )
如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )| A. | 2π | B. | 2π-$\sqrt{3}$ | C. | 2π-2$\sqrt{3}$ | D. | 2π-3$\sqrt{3}$ |
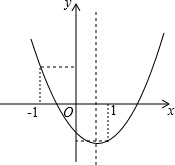 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①点(-ab,c)在第四象限;②a+b+c<0;③$\frac{a+c}{b}$>1;④2a+b>0.其中正确的是①②④.(把所有正确结论的序号都选上)
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①点(-ab,c)在第四象限;②a+b+c<0;③$\frac{a+c}{b}$>1;④2a+b>0.其中正确的是①②④.(把所有正确结论的序号都选上) 如图,AB=CB,∠ABC=60°,且∠EAB=∠FCB,∠ABC=∠FBE,∠CEB=30°.
如图,AB=CB,∠ABC=60°,且∠EAB=∠FCB,∠ABC=∠FBE,∠CEB=30°. 如图所示是一个几何体从上面看到的图形,中间的数字表示该位置的小立方块的个数,请画出这个几何体从正面和左面看到的图形.
如图所示是一个几何体从上面看到的图形,中间的数字表示该位置的小立方块的个数,请画出这个几何体从正面和左面看到的图形.