题目内容
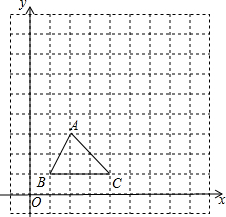
17.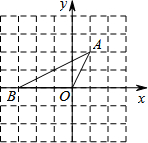 如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.
如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.(1)画出△OA′B′,点A的对应点A′的坐标是(2,-1);
(2)若点P是在y轴上的一个动点,当PA+PA′的值最小时,点P的坐标是(0,1).
分析 (1)根据网格结构找出点A、B旋转后的对应点A′、B′的位置,再与点O顺次连接即可,根据平面直角坐标系写出点A′的坐标即可;
(2)先找出点A关于y轴的对称点A″的位置,连接A′A″与y轴相交,根据轴对称确定最短路线问题,点P即为所求作,再根据图形写出点P的坐标即可.
解答 解:(1)如图所示,△OA′B′即为所作,A′的坐标是(2,-1);
(2)作点A关于y轴的对称点A″的位置,连接A′A″与y轴相交,
根据轴对称确定最短路线问题,点P即为所求作,点P的坐标(0,1),
故答案为(0,1).
点评 本题考查了利用旋转变换作图,轴对称确定最短路线问题,平面直角坐标系中点的坐标的写法,是基础题,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
5.用配方法解方程:x2-4x+1=0,下列配方正确的是( )
| A. | (x-2)2=3 | B. | (x+2)2-3=0 | C. | (x-2)2=0 | D. | x(x-4)=-1 |
12.下列图形中,随机抽取一张是轴对称图形的概率是( )


| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
2.观察数表:
根据数表排列的规律,第n行从右向左数的第5个数是n2+2n-4. (用正整数n表示)
| 第1行 | 1 2 3 |
| 第2行 | 4 5 6 7 8 |
| 第3行 | 9 10 11 12 13 14 15 |
| 第4行 | 16 17 18 19 20 21 22 23 24 |
| … | … |
16.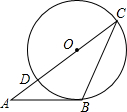 如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.如果∠A=34°,那么∠C等于( )
如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.如果∠A=34°,那么∠C等于( )
 如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.如果∠A=34°,那么∠C等于( )
如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.如果∠A=34°,那么∠C等于( )| A. | 28° | B. | 33° | C. | 34° | D. | 56° |
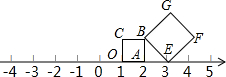 已知正方形OABC,BEFG,按照如图所示位置摆放在数轴上,点O、A、E表示的数分别为1、2、3,若以O为圆心,OF为半径作圆弧,则与数轴的交点表示的数为$\sqrt{10}+1$、-$\sqrt{10}+1$.
已知正方形OABC,BEFG,按照如图所示位置摆放在数轴上,点O、A、E表示的数分别为1、2、3,若以O为圆心,OF为半径作圆弧,则与数轴的交点表示的数为$\sqrt{10}+1$、-$\sqrt{10}+1$.
 如图,在边长为1个单位长度的小正方形网格中:
如图,在边长为1个单位长度的小正方形网格中: