题目内容
9．
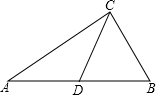如图，在Rt△ABC中，∠BCA=90°，点D为AB上一点，连接CD，AD=BD，CD=CB，则∠A的度数是（ ）| A． | 20° | B． | 30° | C． | 35° | D． | 25° |
分析 由直角三角形斜边的中线等于斜边的一半，可得出CD=BD，结合CD=CB，即可得出△BCD为等边三角形，根据等边三角形的性质结合三角形内角和即可得出∠A的度数．
解答 解：∵∠BCA=90°，AD=BD，
∴CD=BD．
∵CD=CB，
∴△BCD为等边三角形，
∴∠B=60°，∠A=180°-∠B-∠BCA=30°．
故选B．
点评 本题考查了直角三角形斜边上的中线、等边三角形的判定与性质以及三角形内角和定理，根据直角三角形斜边的中线等于斜边的一半结合CD=CB，找出△BCD为等边三角形是解题的关键．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
19．下列式子中，属于最简二次根式的是（ ）
| A． | $\sqrt{13}$ | B． | $\sqrt{20}$ | C． | $\sqrt{8}$ | D． | $\frac{1}{\sqrt{2}}$ |
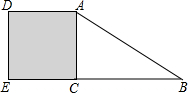如图，在Rt△ACB中，∠ACB=90°，以AC为边向外作正方形ADEC，若图中阴影部分的面积为36cm2，BC=8cm，则AB=10cm．
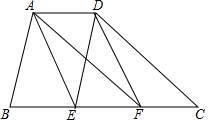如图，在四边形ABCD中，AD∥BC，点E、F在边BC上，DE∥AB，AF∥DC，且AE∥DF．