题目内容
1.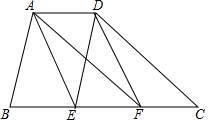 如图,在四边形ABCD中,AD∥BC,点E、F在边BC上,DE∥AB,AF∥DC,且AE∥DF.
如图,在四边形ABCD中,AD∥BC,点E、F在边BC上,DE∥AB,AF∥DC,且AE∥DF.(1)AD与BC有何数量关系?请说明理由;
(2)当四边形ABCD满足条件AB=DC时,四边形AEFD是矩形,请说明理由.
(3)当四边形ABCD满足条件∠B=∠C=45°时,四边形AEFD是正方形(只写结论,不需证明).
分析 (1)感觉平行四边形的判定和性质即可得到结论;
(2)根据矩形的判定定理即可得到结论;
(3)根据正方形的判定定理即可得到结论.
解答 解:(1)AD=$\frac{1}{3}$BC,
理由:∵AD∥BC,DE∥AB,AF∥DC,AE∥DF,
∴四边形ABED,四边形AEFD,四边形AFCD是平行四边形,
∴AD=BE=EF=CF,
∴AD=$\frac{1}{3}$BC;
(2)当四边形ABCD满足条件AB=CD时,四边形AEFD是矩形,
理由:∵AB=CD,
∵四边形ABED,四边形AFCD是平行四边形,
∴AB=DE,AF=CD,
∴DE=AF,
∵四边形AEFD是平行四边形,
∴四边形AEFD是矩形;
(3)当四边形ABCD满足条件∠B=∠C=45°时,四边形AEFD是正方形,
理由:∵AF∥CD,
∴∠AFB=∠C=45°,
∴∠BAF=90°,
∴BA⊥AF,
∵AB∥DF,
∴AF⊥DE,
∴矩形AEFD是正方形.
故答案为:AB=CD,∠B=∠C=90°.
点评 本题考查了平行四边形的判定和性质,矩形的判定和性质,正方形的判定,熟练掌握平行四边形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.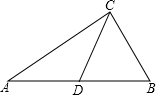 如图,在Rt△ABC中,∠BCA=90°,点D为AB上一点,连接CD,AD=BD,CD=CB,则∠A的度数是( )
如图,在Rt△ABC中,∠BCA=90°,点D为AB上一点,连接CD,AD=BD,CD=CB,则∠A的度数是( )
 如图,在Rt△ABC中,∠BCA=90°,点D为AB上一点,连接CD,AD=BD,CD=CB,则∠A的度数是( )
如图,在Rt△ABC中,∠BCA=90°,点D为AB上一点,连接CD,AD=BD,CD=CB,则∠A的度数是( )| A. | 20° | B. | 30° | C. | 35° | D. | 25° |
12.某市出租车收费标准如下表所示,根据此收费标准,解决下列问题:.
(1)若行驶路程为5km,则打车费用为11.2元;
(2)若行驶路程为x(km)(x>6),则打车费用为(2.4x-1.6)元;(用含x的代数式表示)
(3)当打车费用为27.2元时,行驶路程为多少千米?
| 行驶里程 | 收费标准 |
| 不超出3km的部分 | 起步价7元,燃油附加费1元 |
| 超出3km不超出6km的部分 | 1.6元/km |
| 超出6km的部分 | 2.4元/km |
(2)若行驶路程为x(km)(x>6),则打车费用为(2.4x-1.6)元;(用含x的代数式表示)
(3)当打车费用为27.2元时,行驶路程为多少千米?
 已知:∠B+∠C=90°,AD∥BC,M,N分别是AD、BC中点,求证:MN=$\frac{1}{2}$(BC-AD).
已知:∠B+∠C=90°,AD∥BC,M,N分别是AD、BC中点,求证:MN=$\frac{1}{2}$(BC-AD).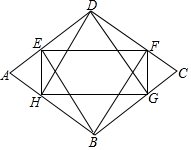 如图,在菱形ABCD中,分别过B、D作对边的垂线,垂足分别为E、F、G、H.若四边形EFGH的面积与菱形ABCD的面积之比为4:9,则sinA=$\frac{2\sqrt{2}}{3}$或$\frac{\sqrt{5}}{3}$.
如图,在菱形ABCD中,分别过B、D作对边的垂线,垂足分别为E、F、G、H.若四边形EFGH的面积与菱形ABCD的面积之比为4:9,则sinA=$\frac{2\sqrt{2}}{3}$或$\frac{\sqrt{5}}{3}$. 在平面直角坐标系中,抛物线y=ax2+bx-3经过点A(-1,0)和点B(2,-1),交y轴于点C,BD⊥x轴于点D,连接AB、AC.
在平面直角坐标系中,抛物线y=ax2+bx-3经过点A(-1,0)和点B(2,-1),交y轴于点C,BD⊥x轴于点D,连接AB、AC. 在哈市地铁2号线的建设中,甲、乙两个建设公司同时挖掘两段长度相等的隧道,如图是甲、乙两公司挖掘隧道长度y(米)与挖掘时间x(时)之间关系的部分图象.如果甲队施工速度始终不变,乙队在开挖6小时后,施工速度每小时增加了7米,结果两队同时完成了任务,那么甲队从开挖到完工所挖隧道的总长度为( )米.
在哈市地铁2号线的建设中,甲、乙两个建设公司同时挖掘两段长度相等的隧道,如图是甲、乙两公司挖掘隧道长度y(米)与挖掘时间x(时)之间关系的部分图象.如果甲队施工速度始终不变,乙队在开挖6小时后,施工速度每小时增加了7米,结果两队同时完成了任务,那么甲队从开挖到完工所挖隧道的总长度为( )米.