题目内容
7.已知点A(a,0)、B(b,0),且(a+4)2+|b-2|=0.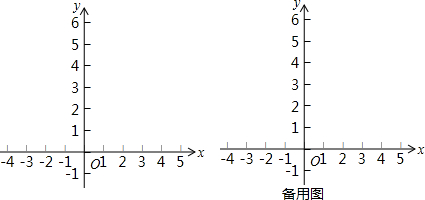
(1)求a、b的值.
(2)在y轴的正半轴上找一点C,使得三角形ABC的面积是15,求出点C的坐标.
(3)过(2)中的点C作直线MN∥x轴,在直线MN上是否存在点D,使得三角形ACD的面积是三角形ABC面积的$\frac{1}{2}$?若存在,求出点D的坐标;若不存在,请说明理由.
分析 (1)根据非负数的性质列方程即可得到结论;
(2)由A(-4,0)、B(2,0),得到AB=6,根据三角形ABC的面积是15列方程即可得到即可;
(3)根据三角形ABC的面积是15列方程即可得到结论.
解答  解:(1)∵(a+4)2+|b-2|=0,
解:(1)∵(a+4)2+|b-2|=0,
∴a+4=0,b-2=0,
∴a=-4,b=2;
(2)如图1,∵A(-4,0)、B(2,0),
∴AB=6,
∵三角形ABC的面积是15,
∴$\frac{1}{2}$AB•OC=15, ∴OC=5,
∴OC=5,
∴C(0,5);
(3)存在,如图2,
∵三角形ABC的面积是15,
∴S△ACD=$\frac{1}{2}$CD•OC=$\frac{1}{2}×$15,
∴$\frac{1}{2}$CD×5=$\frac{1}{2}×$15,
∴CD=3,
∴D(3.5)或(-3,5).
点评 本题考查了坐标于图形的性质,非负数的性质,三角形的面积,正确的作出图形是解题的关键.

练习册系列答案
相关题目
18.下列计算结果正确的是( )
| A. | (-a3)2=a9 | B. | a6÷a3=a2 | C. | (-$\frac{1}{2}$)-1=-2 | D. | (cos60°-$\frac{1}{2}$)0=1 |
12.下列计算正确的是( )
| A. | (-4x)•(2x2+3x-1)=-8x3-12x2-4x | |
| B. | (6xy2-4x2y)•3xy=6xy2-12x3y2 | |
| C. | (-x)•(2x+x2-1)=-x3-2x2+1 | |
| D. | (-3x2y)(-2xy+3yz+1)=6x3y2-9x2y2z-3x2y |
 如图,将一块含45°的直角三角板的直角顶点放在直尺的一边上,∠1=75°,则∠2的度数是30°.
如图,将一块含45°的直角三角板的直角顶点放在直尺的一边上,∠1=75°,则∠2的度数是30°. 如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.
如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.