题目内容
5．
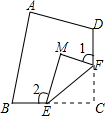如图，四边形ABCD，∠C=90°，E在BC上，F在CD上，将△EFC沿EF折叠，得到△EFM，则图中∠1+∠2=180度．
分析 由翻折的性质得：∠M=∠C=90°，由四边形的内角和公式求出∠MEC+∠MFC=180°，由∠1=180°-∠MFC，∠2=180°-∠MEC，代入即可求得结论．
解答 由翻折的性质得：∠M=∠C=90°，
∴∠MEC+∠MFC=360-∠M-∠C=180°，
∵∠1=180°-∠MFC，∠2=180°-∠MEC，
∴∠1+∠2=180°-∠MFC+180°-∠MEC=360°-（∠MEC+∠MFC）=360°-180°=180°，
故答案为：180°．
点评 本题主要考查了翻折的性质，多边形的内角和公式，整体代入思想，能灵活应用翻折的性质是解决问题的关键．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
如图，已知AB是⊙O的直径，OD⊥AC，OD=3，则弦BC的长为6．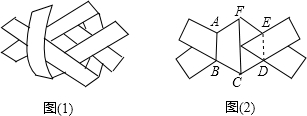
用两条宽均为2cm的纸条（假设纸条的长度足够长），折叠穿插，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正六边形ABCDEF，则折出的正六边形的边长为$\frac{4\sqrt{3}}{3}$cm．
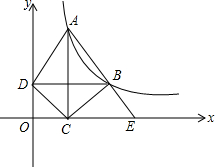如图，反比例函数y=$\frac{k}{x}$（x＞0，k≠0）的图象经过点A（1，6），过点A作AC⊥x轴于点C，点B在直线AC右侧的函数图象上，过点B作BD⊥y轴于点D，交AC于点F，连接BC、AD、CD．