题目内容
5.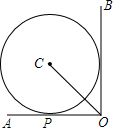 如图,⊙C与∠AOB的两边分别相切,其中OA边与⊙C相切于点P.若∠AOB=90°,OP=6,则OC的长为( )
如图,⊙C与∠AOB的两边分别相切,其中OA边与⊙C相切于点P.若∠AOB=90°,OP=6,则OC的长为( )| A. | 12 | B. | $12\sqrt{2}$ | C. | $6\sqrt{2}$ | D. | $6\sqrt{3}$ |
分析 连接CP,由切线的性质可得CP⊥AO,再由切线长定理可得∠POC=45°,进而可得△POC是等腰直角三角形,利用勾股定理即可求出OC的长.
解答 解:
连接CP,
∵OA边与⊙C相切于点P,
∴CP⊥AO,
∵⊙C与∠AOB的两边分别相切,∠AOB=90°,
∴∠POC=45°,
∴OP=CP=6,
∴OC=$\sqrt{C{P}^{2}+O{P}^{2}}$=6$\sqrt{2}$,
故选C.
点评 本题考查了切线的性质定理、切线长定理以及勾股定理的运用,能够正确的判定△POC是等腰直角三角形是解题关键.

练习册系列答案
相关题目
13.下列实数中是无理数的是( )
| A. | 0.38 | B. | $\root{3}{9}$ | C. | $\sqrt{36}$ | D. | -$\frac{22}{7}$ |
20.口袋里有除颜色不同外其它都相同的红、蓝、白三种颜色的小球共30个,摸到红球的概率是$\frac{1}{2}$,摸到蓝球的概率是$\frac{1}{3}$,则袋子里有白球( )个.
| A. | 15 | B. | 10 | C. | 5 | D. | 6 |
10.⊙O的半径为7cm,点P到圆心O的距离OP=10cm,则点P与圆O的位置关系为( )
| A. | 点P在圆上 | B. | 点P在圆内 | C. | 点P在圆外 | D. | 无法确定 |
17.有一组单项式:a2,-$\frac{{a}^{3}}{2}$,$\frac{{a}^{4}}{3}$,-$\frac{{a}^{5}}{4}$…,请观察它们的构成规律,用你发现的规律写出第10个单项式为( )
| A. | $\frac{{a}^{10}}{10}$ | B. | -$\frac{{a}^{10}}{10}$ | C. | $\frac{{a}^{11}}{10}$ | D. | -$\frac{{a}^{11}}{10}$ |
 如图,AB是半圆的直径,将半圆绕点B顺时针旋转45°,点A旋转到A′的位置,已知图中阴影部分的面积为4π,则点A旋转的路径长为$\sqrt{2}π$.
如图,AB是半圆的直径,将半圆绕点B顺时针旋转45°,点A旋转到A′的位置,已知图中阴影部分的面积为4π,则点A旋转的路径长为$\sqrt{2}π$. 一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是6.
一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是6.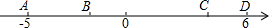 如图,数轴上有A,B,C,D四个整数点(即各点均表示整数),且2AB=BC=3CD.若A,D两点所表示的数分别是-5和6,则线段BD的中点所表示的数是( )
如图,数轴上有A,B,C,D四个整数点(即各点均表示整数),且2AB=BC=3CD.若A,D两点所表示的数分别是-5和6,则线段BD的中点所表示的数是( )