题目内容

15．如图，AB是半圆的直径，将半圆绕点B顺时针旋转45°，点A旋转到A′的位置，已知图中阴影部分的面积为4π，则点A旋转的路径长为$\sqrt{2}π$．

分析 根据图形得到S阴影=S半圆+S扇形-S半圆=4π，求得AB=4$\sqrt{2}$，然后根据弧长的计算公式即可得到结论．

解答 解：∵S阴影=S半圆+S扇形-S半圆=4π，
∴$\frac{45π•A{B}^{2}}{360}$=4π，
∴AB=4$\sqrt{2}$，
∴点A旋转的路径长=$\frac{45•π×4\sqrt{2}}{180}$=$\sqrt{2}π$，
故答案为：$\sqrt{2}π$．

点评 本题考查了弧长的计算，扇形的面积的计算，旋转的性质，熟记弧长的计算公式是解题的关键．

练习册系列答案
相关题目
5．如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．
（1）△ABC向右平移4个单位得到△A1B1C1，请画出△A1B1C1；
（2）请以△ABC的B点为位似中心画相似三角形，使得该三角形与△ABC的相似比为1：2．
6．如果用-10%表示某商品的出口额比上一年减少10%，那么+12%则表示该商品的出口额比上一年（　　）
A．增加2%B．增加12%C．减少12%D．减少22%
3．对于三个数a、b、c，M|a，b，c|表示这三个数的平均数，min {a，b，c}表示a、b、c这三个数中最小的数，如：M|-1，2，3|=$\frac{-1+2+3}{3}$=$\frac{4}{3}$，min {-1，2，3}=-1；
M|-1，2，a|=$\frac{-1+2+a}{3}$=$\frac{a+1}{3}$，min{-1，2，a}=$\left\{\begin{array}{l}{a（a≤-1）}\\{-1（a＞-1）}\end{array}\right.$
解决下列问题：
（1）填空：M|$-\sqrt{8}$，$\sqrt{2}$，$\sqrt{18}$|=$\frac{2}{3}$$\sqrt{2}$；min{-3，$-\sqrt{5}$，-π}=-π；
（2）若min{2，2x+2，4-2x}=2，求x的取值范围；
（3）若M|2，x+1，2x|=min{2，x+1，2x}，求x的值；
（4）如图，在同一平面直角坐标系中，画出了函数y=x+1，y=（x-1）2，y=2-x的图象，则min{x+1，（x-1）2，2-x}的最大值为1．
10．在Rt△ABC中，∠C=90°，BC=3，AB=4，则sinA的值为（　　）
A．$\frac{3}{5}$B．$\frac{4}{5}$C．$\frac{3}{4}$D．$\frac{4}{3}$
20．若2a-b=1，则代数式4a-2b-1的值是1．
7．下列计算正确的是（　　）
A．a+a=a2B．3a2-2a3=1C．3a3-2a2=aD．-a2+2a2=a2
4．下列图形中是轴对称图形的为（　　）
A．B．C．D．
5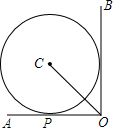．如图，⊙C与∠AOB的两边分别相切，其中OA边与⊙C相切于点P．若∠AOB=90°，OP=6，则OC的长为（　　）
A．12B．$12\sqrt{2}$C．$6\sqrt{2}$D．$6\sqrt{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网