题目内容
18．
如图，以正六边形ADHGFE的一边AD为边向外作正方形ABCD，则∠BED的度数为（ ）| A． | 30° | B． | 45° | C． | 50° | D． | 60° |
分析 根据正六边形ADHGFE的内角为120°，正方形ABCD的内角为90°，求出∠BEA=30°，∠AED=30°，据此即可解答．
解答 解：∵正六边形ADHGFE的内角为120°，
正方形ABCD的内角为90°，
∴∠BAE=360°-90°-120°=150°，
∵AB=AE，
∴∠BEA=$\frac{1}{2}$×（180°-150°）=15°，
∵∠DAE=120°，AD=AE，
∴∠AED=$\frac{180°-120°}{2}$=30°，
∴∠BED=15°+30°=45°．
故选B．
点评 本题考查了正多边形和圆，熟悉正多边形的性质是解题的关键．
练习册系列答案
相关题目
9．若代数式5x2-4x+6的值为26，则${x^2}-\frac{4}{5}x+6$的值为（ ）
| A． | 6 | B． | 10 | C． | 14 | D． | 30 |
13．方程3-2（x-5）=9的解是（ ）
| A． | x=-2 | B． | x=2 | C． | x=$\frac{2}{3}$ | D． | x=1 |
3．
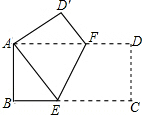如图，在矩形ABCD中，AB=4，BC=8，将矩形ABCD沿EF折叠，使点C与A重合，则折痕EF的长为（ ）
如图，在矩形ABCD中，AB=4，BC=8，将矩形ABCD沿EF折叠，使点C与A重合，则折痕EF的长为（ ）| A． | 5 | B． | 6 | C． | 5$\sqrt{2}$ | D． | 2$\sqrt{5}$ |
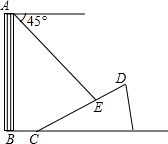如图，一楼房AB后有一假山，其斜坡CD坡比为1：$\sqrt{3}$，山坡坡面上点 E处有一休息亭，测得假山坡脚C与楼房水平距离BC=25米，与亭子距离CE=20米，小丽从楼房顶测得点E的俯角为45°．