题目内容
6.化简、计算:$\sqrt{18}$=3$\sqrt{2}$;$\sqrt{1\frac{1}{2}}$=$\frac{\sqrt{6}}{2}$;$(2\sqrt{3})^{2}$=12.
分析 直接利用二次根式的性质化简求出即可.
解答 解:$\sqrt{18}$=3$\sqrt{2}$;$\sqrt{1\frac{1}{2}}$=$\sqrt{\frac{3}{2}}$=$\frac{\sqrt{6}}{2}$;$(2\sqrt{3})^{2}$=12.
故答案为:3$\sqrt{2}$,$\frac{\sqrt{6}}{2}$,12.
点评 此题主要考查了二次根式的乘除以及二次根式的化简,正确掌握二次根式的性质是解题关键.

练习册系列答案
相关题目
1.下列算式中,正确的有( )
| A. | $\sqrt{3}$+$\sqrt{4}$=$\sqrt{7}$ | B. | 3$\sqrt{2}$-2$\sqrt{2}$=-$\sqrt{2}$ | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{1\frac{1}{2}}$÷$\sqrt{\frac{1}{6}}$=3 |
18. 如图,以正六边形ADHGFE的一边AD为边向外作正方形ABCD,则∠BED的度数为( )
如图,以正六边形ADHGFE的一边AD为边向外作正方形ABCD,则∠BED的度数为( )
 如图,以正六边形ADHGFE的一边AD为边向外作正方形ABCD,则∠BED的度数为( )
如图,以正六边形ADHGFE的一边AD为边向外作正方形ABCD,则∠BED的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
16.下列各数中,比-2大的数是( )
| A. | -3 | B. | 0 | C. | -2 | D. | -2.1 |
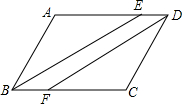 如图,四边形ABCD是平行四边形,BE平分∠ABC,DF平分∠ADC,求证:四边形DEBF是平行四边形.
如图,四边形ABCD是平行四边形,BE平分∠ABC,DF平分∠ADC,求证:四边形DEBF是平行四边形. 如图,在?ABCD中,∠ADC的角平分线DE交AC于点F,AE=2,则AD=2.
如图,在?ABCD中,∠ADC的角平分线DE交AC于点F,AE=2,则AD=2.