题目内容
7.已知一次函数y=mx+b(m<0)与反比例函数y=$\frac{k}{x}$相交于点A(1,3)及点B,当△AOB的面积为4时,求m的值.分析 先由反比例函数y=$\frac{k}{x}$的图象过点A(1,3),得出k=1×3=3,于是可设点B的坐标为(a,$\frac{3}{a}$).再作AE⊥x轴,BF⊥x轴,垂足分别为E、F,根据反比例函数比例系数k的几何意义得出S△AOB=S四边形AEFB=4,依此列出方程$\frac{1}{2}$($\frac{3}{a}$+3)×(a-1)=4,求出a的值,然后把A(1,3),B(3,1)代入y=mx+b,即可求出m的值.
解答 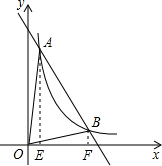 解:∵反比例函数y=$\frac{k}{x}$的图象过点A(1,3),
解:∵反比例函数y=$\frac{k}{x}$的图象过点A(1,3),
∴k=1×3=3,
∴反比例函数的解析式为y=$\frac{3}{x}$,
∴可设点B的坐标为(a,$\frac{3}{a}$).
作AE⊥x轴,BF⊥x轴,垂足分别为E、F,则S△AOE=S△BOF=1.5,
∵S△AOB=S四边形AEFB+S△AOE-S△BOF=S四边形AEFB=4,
∴$\frac{1}{2}$($\frac{3}{a}$+3)×(a-1)=4,
整理得,3a2-8a-3=0,
解得a1=3,a2=-$\frac{1}{3}$(不合题意舍去),
∴点B的坐标为(3,1).
把A(1,3),B(3,1)代入y=mx+b,
得$\left\{\begin{array}{l}{m+b=3}\\{3m+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-1}\\{b=4}\end{array}\right.$,
故所求m的值为-1.
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法求反比例函数与一次函数的解析式,反比例函数$y=\frac{k}{x}$中k的几何意义,三角形的面积,体现了数形结合的思想.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,以正六边形ADHGFE的一边AD为边向外作正方形ABCD,则∠BED的度数为( )
如图,以正六边形ADHGFE的一边AD为边向外作正方形ABCD,则∠BED的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
| A. | -3 | B. | 0 | C. | -2 | D. | -2.1 |
 如图,在?ABCD中,∠ADC的角平分线DE交AC于点F,AE=2,则AD=2.
如图,在?ABCD中,∠ADC的角平分线DE交AC于点F,AE=2,则AD=2. 在平面直角坐标系中,描出下列3个点:A (-1,0),把点A向右平移2个单位,再向上平移4个单位得到点B,点C 的坐标是(4,2);
在平面直角坐标系中,描出下列3个点:A (-1,0),把点A向右平移2个单位,再向上平移4个单位得到点B,点C 的坐标是(4,2);  已知:如图,求作△ABC的高AD、角平分线BE、中线CF.
已知:如图,求作△ABC的高AD、角平分线BE、中线CF.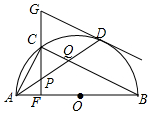 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CF⊥AB于点E,过点D的切线交FC的延长线于点G,连接AD,分别交CF、CB于点P、Q,连接AC.给出下列结论:①∠BAD=∠ABC;②AD=CB;③点P是△ACQ的外心;④GP=GD;⑤CB∥GD.其中正确结论的序号是( )
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CF⊥AB于点E,过点D的切线交FC的延长线于点G,连接AD,分别交CF、CB于点P、Q,连接AC.给出下列结论:①∠BAD=∠ABC;②AD=CB;③点P是△ACQ的外心;④GP=GD;⑤CB∥GD.其中正确结论的序号是( )