题目内容
17.已知,正方形ABCD,点P在对角线BD上,连接AP、CP(如图①)(1)求证:AP=CP.
(2)将一直角三角板的直角顶点置于点P处并绕点P旋转,设两直角边分别交DC、BC于E、F,
a.若旋转到图②位置,使PE与PA在一直线上,求证:PF=PA.
b.若旋转到图③位置且PD:PB=2:3,求PE:PF的值.

分析 (1)先根据正方形的性质得出结论判断出△ABP≌△CBP,即可;
(2)a、连接PC,利用三角形的外角和直角得出∠PFC=135°-∠APB,∠PCF=135°-∠APB,从而得出∠PFC=∠PCF,即可得出PF=PC,借助(1)结论即可;
b、先构造出直角三角形,得出PG=$\frac{\sqrt{2}}{2}$BP,PH=$\frac{\sqrt{2}}{2}$DP,再判断出△PGF∽PHE,得出$\frac{PE}{PF}=\frac{PH}{PG}$代入即可.
解答 解:(1)∵BD是正方形ABCD的对角线,
∴AB=BC,∠ABD=∠CBD=45°,
在△ABP和△CBP中,$\left\{\begin{array}{l}{AB=CB}\\{∠ABD=∠CBD}\\{AP=AP}\end{array}\right.$,
∴△ABP≌△CBP,
∴AP=CP,
(2)a、如图②,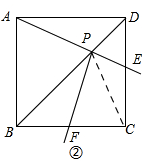 连接PC,
连接PC,
∵∠CBD=45°,
∴∠PFC=∠CBD+∠BPF=45°+∠BPF,
∵∠EPF=∠APF=90°,
∴∠BPF+∠APB=90°,
∴∠BPF=90°-∠APB,
∴∠PFC=135°-∠APB
∵∠APB=∠DAP+∠ADB=45°+∠DAP,
同(1)的方法得出△PAD≌△PCD,
∴∠DAP=∠DCP,
∴∠APB=45°+∠DCP,
∵∠PCF+∠DCP=90°,
∴∠PCF=90°-∠DCP=90°-(∠APB-45°)=135°-∠APB,
∴∠PFC=∠PCF,
∴PF=PC,
由(1)知,PA=PC,
∴PF=PA.
b、如图③,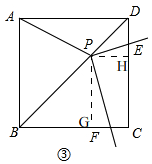
过点P作PG⊥BC,
∵∠CBD=45°,
∴PG=$\frac{\sqrt{2}}{2}$BP,
过点P作PH⊥CD,
同理:PH=$\frac{\sqrt{2}}{2}$DP,
∵∠C=∠PFC=∠PHC=90°,
∴∠HPG=90°,
∵∠EPF=90°,
∴∠FPG=∠EPH,
∵∠PFC=∠PHC=90°,
∴△PGF∽PHE,
∴$\frac{PE}{PF}=\frac{PH}{PG}$=$\frac{\frac{\sqrt{2}}{2}DP}{\frac{\sqrt{2}}{2}BP}$=$\frac{DP}{BP}$,
∵PD:PB=2:3
∴$\frac{PE}{PF}$=$\frac{2}{3}$.
点评 此题是四边形综合题,主要考查了正方形的性质,四边形的内角和(也可以先判断矩形得出∠HPG=90°),直角三角形的性质,相似三角形的判定和性质,解本题的关键是得出PF=PC,难点是构造直角三角形.

 阅读快车系列答案
阅读快车系列答案 如图,菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(0,2$\sqrt{3}$),∠DOB=60°,点P是对角线OC上的一个动点,已知A(-1,0),则AP+BP的最小值为( )
如图,菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(0,2$\sqrt{3}$),∠DOB=60°,点P是对角线OC上的一个动点,已知A(-1,0),则AP+BP的最小值为( )| A. | 4 | B. | 5 | C. | 3$\sqrt{3}$ | D. | $\sqrt{19}$ |
| A. | m≥-4 | B. | m>4 | C. | m<-4 | D. | m≤-4 |

| A. | (1 )(2) | B. | (1)(4) | C. | (2)(3) | D. | (3)(4) |
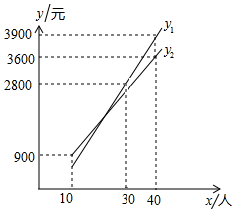 2016年3月28日,农业部发布了以“早春到乡村去踏青”为主题的219条休闲农业精品景点线路,其中河北省的“唐山迁西滨水度假游”等20条休闲农业精品线路入选.已知河北省某旅游景点的门票为a元/人,为吸引团队游客,对团队10人以上(包含10人)的游客实行动态票价:节假日期间门票不打折,但会在团队总费用的基础上有优惠;非节假日期间门票打b折.某团队在节假日期间的门票总费用y1(元)、非节假日期间的门票总费用y2(元)与团队人数x(人)(x≥10)之间的函数关系的图象如图所示.
2016年3月28日,农业部发布了以“早春到乡村去踏青”为主题的219条休闲农业精品景点线路,其中河北省的“唐山迁西滨水度假游”等20条休闲农业精品线路入选.已知河北省某旅游景点的门票为a元/人,为吸引团队游客,对团队10人以上(包含10人)的游客实行动态票价:节假日期间门票不打折,但会在团队总费用的基础上有优惠;非节假日期间门票打b折.某团队在节假日期间的门票总费用y1(元)、非节假日期间的门票总费用y2(元)与团队人数x(人)(x≥10)之间的函数关系的图象如图所示. 小颖利用计算机画出了函数y=x3-3x2-x+4的图象(如图),根据图象,你能求得方程x3-3x2-x+4=0的近似根吗?请写出你的结果,并说出你的理由(结果保留小数点后一位)
小颖利用计算机画出了函数y=x3-3x2-x+4的图象(如图),根据图象,你能求得方程x3-3x2-x+4=0的近似根吗?请写出你的结果,并说出你的理由(结果保留小数点后一位) 如图,在平行四边形ABCD中,AC⊥AB,以C为圆心,CA为半径作圆弧交BC于点E,交CD的延长线于点F,以AC上一点O为圆心,OA为半径的圆与BC相切于点G,交AD于点N,若AC=6cm,OA=2cm,则图中阴影部分的面积为 $\frac{23}{3}π-5\sqrt{3}$,cm2(结果不取近似值).
如图,在平行四边形ABCD中,AC⊥AB,以C为圆心,CA为半径作圆弧交BC于点E,交CD的延长线于点F,以AC上一点O为圆心,OA为半径的圆与BC相切于点G,交AD于点N,若AC=6cm,OA=2cm,则图中阴影部分的面积为 $\frac{23}{3}π-5\sqrt{3}$,cm2(结果不取近似值).