题目内容
7. 如图,在平行四边形ABCD中,AC⊥AB,以C为圆心,CA为半径作圆弧交BC于点E,交CD的延长线于点F,以AC上一点O为圆心,OA为半径的圆与BC相切于点G,交AD于点N,若AC=6cm,OA=2cm,则图中阴影部分的面积为 $\frac{23}{3}π-5\sqrt{3}$,cm2(结果不取近似值).
如图,在平行四边形ABCD中,AC⊥AB,以C为圆心,CA为半径作圆弧交BC于点E,交CD的延长线于点F,以AC上一点O为圆心,OA为半径的圆与BC相切于点G,交AD于点N,若AC=6cm,OA=2cm,则图中阴影部分的面积为 $\frac{23}{3}π-5\sqrt{3}$,cm2(结果不取近似值).
分析 先求出∠ACD=90°,∠AOM=120°,再分别求出S扇形ACF,S扇形AON,S△ACD,S△AON最后求面积的和差即可
解答 解:如图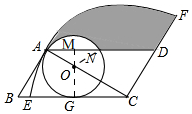 ,
,
连接ON,OG,并延长GO交AD于M,
在Rt△OGC中,OC=4,OG=2,
∴∠OCG=30°,
∵AD∥BC,
∴∠CAD=30°,
∵OA=ON,
∴∠CAD=∠ANO=30°,
在Rt△OAM中,OM=$\frac{1}{2}$OA=1,AM=$\sqrt{O{A}^{2}-O{M}^{2}}$=$\sqrt{3}$,
在Rt△ACD中,CD=ACtan30°=2$\sqrt{3}$,
∴S扇形ACF=$\frac{90π×{6}^{2}}{360}$=9π,
S扇形AON=$\frac{120π×{2}^{2}}{360}$=$\frac{4}{3}$π,
S△ACD=$\frac{1}{2}$AC×CD=6$\sqrt{3}$,
S△AON=$\frac{1}{2}$AN×OM=$\sqrt{3}$,
∴S阴影=S扇形ACF-S△ACD-S扇形AON+S△AON=9π-6$\sqrt{3}$-$\frac{4}{3}π$+$\sqrt{3}$=$\frac{23}{3}π-5\sqrt{3}$cm2.
故答案为$\frac{23}{3}π-5\sqrt{3}$.
点评 此题是切线的性质,主要考查了不规则图形面积的求法,通常化成几个规则图形面积,涉及扇形的面积的计算,弓形,三角形面积的计算,熟记基本图形计算面积的公式是解本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
16.已知某公司去年的营业额约为四千零七十万元,则此营业额可表示为( )
| A. | 4.07×105元 | B. | 4.07×106元 | C. | 4.07×107元 | D. | 4.07×108元 |



 利用二次函数y=x2-5x+5的图象,探索方程x2-5x+5=0的介于1~2之间的根(精确到0.1).
利用二次函数y=x2-5x+5的图象,探索方程x2-5x+5=0的介于1~2之间的根(精确到0.1).