��Ŀ����
12����֪��ABC�У���A=x��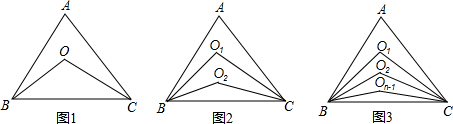
��1����ͼ1������ABC�͡�ACB�Ľ�ƽ�����ཻ�ڵ�O�����ú�x�Ĵ���ʽ��ʾ��BOC��д���������̣�
��2����ͼ2������ABC�͡�ACB�����ȷ����ཻ�ڵ�O1��O2�����ú�x�Ĵ���ʽ��ʾ��BO1C��д���������̣�
��3����ͼ3������ABC�͡�ACB��n�ȷ����ཻ�ڵ�O1��O2������On-1�����ú�n��x�Ĵ���ʽ��ʾ��BO1C������Ҫ�������̣�ֱ��д�������
���� ��1���ɡ�ABC�͡�ACB�Ľ�ƽ�����ཻ�ڵ�O���ã�2��OBC=��ABC��2��OCB=��ACB�������������ڽǺͶ������ɵã���A+2��OBC+2��OCB=180�㣬��BOC+��OBC+��OCB=180�㣬������á�BOC��ֵ��
��2���ɡ�ABC�͡�ACB�����ȷ����ཻ�ڵ�O1��O2�����ɵá�O1BC=$\frac{2}{3}$��ABC����O1CB=$\frac{2}{3}$��ACB�������������ڽǺͶ������ɵã���A+$\frac{3}{2}$��O1BC+$\frac{3}{2}$��O1CB=180�㣬��BO1C+��O1BC+��O1CB=180�㣬������á�BO1C��ֵ��
��3���۲죨1����2�������ɵù��ɣ�����ABC�͡�ACB��n�ȷ����ཻ�ڵ�O1��O2������On-1��
���BO1C=��$\frac{180}{n}$+$\frac{n-1}{n}$x����
��� �⣺��1���ߡ�ABC�͡�ACB�Ľ�ƽ�����ཻ�ڵ�O��
��2��OBC=��ABC��2��OCB=��ACB��
�ߡ�A+��ABC+��ACB=180�㣬
���A+2��OBC+2��OCB=180�㣬
���OBC+��OCB=90��-$\frac{1}{2}$��A��
�ߡ�BOC=180��-����OBC+��OCB��=90��+$\frac{1}{2}$��A��
�ߡ�A=x�㣬
���BOC=��90+$\frac{1}{2}$x���㣻
��2���ߡ�ABC�͡�ACB�����ȷ����ཻ�ڵ�O1��O2��
���O1BC=$\frac{2}{3}$��ABC����O1CB=$\frac{2}{3}$��ACB��
��$\frac{3}{2}$��O1BC=��ABC��$\frac{3}{2}$��O1CB=��ACB��
�ߡ�A+��ABC+��ACB=180�㣬
���A+$\frac{3}{2}$��O1BC+$\frac{3}{2}$��O1CB=180�㣬
���O1BC+��O1CB=$\frac{2}{3}$��180��-��A����
�ߡ�BOC=180��-����O1BC+��O1CB��=60��+$\frac{2}{3}$��A��
�ߡ�A=x�㣬
���BOC=��60+$\frac{2}{3}$x���㣻
��3���ɣ�1����2���ɵù���Ϊ��
����ABC�͡�ACB��n�ȷ����ཻ�ڵ�O1��O2������On-1��
����x��ʾ��BO1C=��$\frac{180}{n}$+$\frac{n-1}{n}$x����
���� ���⿼���˽ǵĵȷ��ߵ������Լ��������ڽǺͶ�����ע���ҵĹ��ɣ�����ABC�͡�ACB��n�ȷ����ཻ�ڵ�O1��O2������On-1������x��ʾ��BO1C=�� $\frac{180}{n}$+$\frac{n-1}{n}$x���㣬�ǽ����Ĺؼ���

 ��У����ϵ�д�
��У����ϵ�д�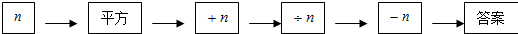
��1�������
| ����n | 3 | $\frac{1}{2}$ | -2 | �� |
| ����� | 1 | 1 | 1 | �� |
| A�� | -3 | B�� | -7 | C�� | 3 | D�� | 7 |
 ��ͼ��������������A��B�������A��ʾ������-3���߶�AB=7����ô��B��ʾ������4��-10��
��ͼ��������������A��B�������A��ʾ������-3���߶�AB=7����ô��B��ʾ������4��-10��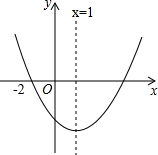 ���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н����У���abc��0��
���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н����У���abc��0��