题目内容
8.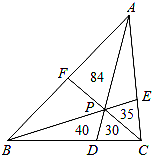 如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,则△ABC的面积为( )
如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,则△ABC的面积为( )| A. | 300 | B. | 315 | C. | 279 | D. | 342 |
分析 根据等高不等底的三角形的面积的比等于底边的比,求解,从而不难求得△ABC的面积.
解答 解:设△BPE的面积为x,△APE的面积为y,
由等高不等底的三角形的面积的比等于底边的比,得:$\frac{40}{84+x}=\frac{30}{35+y}$,①
$\frac{35}{30+40}$=$\frac{y}{84+x}$,②
两式联立解得:x=56,y=70,
∴△ABC的面积=84+70+35+40+30+56=315.
故选B.
点评 本题考查三角形面积的知识,难度不大,关键是设出未知三角形的面积,然后根据等高不等底的三角形的面积的比等于底边的比列式求解.

练习册系列答案
相关题目
16.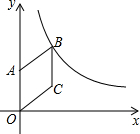 如图,在平面直角坐标系中,菱形OABC的顶点A在y轴的正半轴上,点B在函数y=$\frac{k}{x}$(x>0)的图象上,若点C的坐标为(4,3),则k的值为( )
如图,在平面直角坐标系中,菱形OABC的顶点A在y轴的正半轴上,点B在函数y=$\frac{k}{x}$(x>0)的图象上,若点C的坐标为(4,3),则k的值为( )
 如图,在平面直角坐标系中,菱形OABC的顶点A在y轴的正半轴上,点B在函数y=$\frac{k}{x}$(x>0)的图象上,若点C的坐标为(4,3),则k的值为( )
如图,在平面直角坐标系中,菱形OABC的顶点A在y轴的正半轴上,点B在函数y=$\frac{k}{x}$(x>0)的图象上,若点C的坐标为(4,3),则k的值为( )| A. | 12 | B. | 20 | C. | 24 | D. | 32 |
17.下列计算中,正确的是( )
| A. | a3+a3=a6 | B. | a3•a2=a6 | C. | (-a3)2=a9 | D. | (-a2)3=-a6 |
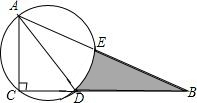 如图,已知△ABC,∠ACB=90°,∠B=30°,AD平分∠BAC,以AD为直径作圆O交AB于E,已知CD=2,则图中阴影部分的面积(用含x的代数式表示)为:2$\sqrt{3}$-$\frac{2}{3}$π.
如图,已知△ABC,∠ACB=90°,∠B=30°,AD平分∠BAC,以AD为直径作圆O交AB于E,已知CD=2,则图中阴影部分的面积(用含x的代数式表示)为:2$\sqrt{3}$-$\frac{2}{3}$π. 某校为了发展校园足球运动,组建了校足球队,队员年龄分布如图所示,则这些队员年龄的众数是14.
某校为了发展校园足球运动,组建了校足球队,队员年龄分布如图所示,则这些队员年龄的众数是14.