题目内容
2.在直角坐标系中,已知点A,B的坐标是(a,0),(b,0).a,b满足方程组$\left\{\begin{array}{l}{2a+b=5}\\{3a-2b=-11}\end{array}\right.$,C为y轴正半轴上一点,且S△ABC=6.(1)求A,B,C三点的坐标;
(2)是否存在点P(t,t),使S△PAB=$\frac{1}{3}$S△ABC?若存在,请求出P点的坐标;若不存在,请说明理由.
分析 (1)解出方程组即可得到时点A,B的坐标,利用S△ABC=6,求出点C的坐标;
(2)利用S△PAB=$\frac{1}{3}$S△ABC求出点P的坐标即可.
解答 解:(1)由方程组$\left\{\begin{array}{l}{2a+b=5}\\{3a-2b=-11}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-3}\\{b=1}\end{array}\right.$,
∴A(-3,0),B(1,0),
∵c为y轴正半轴上一点,且S△ABC=6,
∴$\frac{1}{2}$AB•OC=6,解得:OC=3
∴C(0,3).
(2)存在.
理由:∵P(t,t),且S△PAB=$\frac{1}{3}$S△ABC,
∴$\frac{1}{2}$×4×|t|=$\frac{1}{3}$×6,
解得t=±1,
∴P(1,1)或(-1,-1).
点评 本题主要考查了坐标与图形性质,三角形的面积和解二元一次方程组,掌握三角形的面积以及分类讨论是解决问题的关键.

练习册系列答案
相关题目
 如图所示,直线L1的解析式是y=2x-1,直线L2的解析式是y=x+1,则方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x-y=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
如图所示,直线L1的解析式是y=2x-1,直线L2的解析式是y=x+1,则方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x-y=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$. x^y
x^y
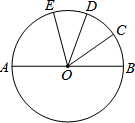 如图,AB是⊙O的直径,$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$,∠COD=35°,则∠AOE=75°.
如图,AB是⊙O的直径,$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$,∠COD=35°,则∠AOE=75°.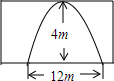 如图是一座抛物线形拱桥,当水面的宽为12m时,拱顶离水面4m,当水面下降2m时,水面的宽为6$\sqrt{6}$m.
如图是一座抛物线形拱桥,当水面的宽为12m时,拱顶离水面4m,当水面下降2m时,水面的宽为6$\sqrt{6}$m.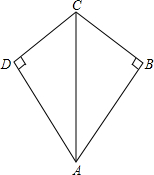 如图,四边形ABCD中,CB=CD,∠B=∠D=90°,∠BAD=60°,则∠ACB的度数为60°.
如图,四边形ABCD中,CB=CD,∠B=∠D=90°,∠BAD=60°,则∠ACB的度数为60°.