题目内容
14．
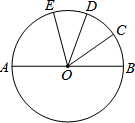如图，AB是⊙O的直径，$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$，∠COD=35°，则∠AOE=75°．
分析 由$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$，根据弧与圆心角的关系，可得∠BOC=∠DOE=∠COD=35°，继而求得答案．
解答 解：∵$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$，
∴∠BOC=∠DOE=∠COD=35°，
∴∠AOE=180°-∠BOC-∠COD-∠DOE=75°．
故答案为：75．
点评 此题考查了弧与圆心角的关系．注意在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
练习册系列答案
全能测控一本好卷系列答案
相关题目
已知点A（0，3），B（-1，1），C（-3，2），D（-2，0），E（-3，-2），F（-1，-1），G（0，-3），H（1，-1），I（3，-2），J（2，0），K（3，2），L（1，1）