Question

11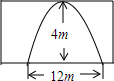．如图是一座抛物线形拱桥，当水面的宽为12m时，拱顶离水面4m，当水面下降2m时，水面的宽为6$\sqrt{6}$m．

Answer 1

分析 根据题意可以建立合适的平面直角坐标系，设出二次函数的顶点式，由图象知抛物线过点（6，0），从而可以求得抛物线的解析式，然后将y=-2代入解析式，即可求得问题的答案．

解答 解：根据题意可以建立合适的平面直角坐标系，如下图所示：

设二次函数的解析式为：y=ax²+4，
∵点（6，0）在抛物线的上，
∴0=a×6²+4
解得a=$-\frac{1}{9}$，
∴y=$-\frac{1}{9}{x}^{2}+4$，
将y=-2代入$y=-\frac{1}{9}{x}^{2}+4$，得${x}_{1}=-3\sqrt{6}，{x}_{2}=3\sqrt{6}$，
∴水面的宽为：$3\sqrt{6}-（-3\sqrt{6}）=6\sqrt{6}$．
故答案为：$6\sqrt{6}$．

点评 本题考查二次函数的应用，解题的关键是画出相应的平面直角坐标系，设出合适的二次函数．