题目内容
1.甲盒子中有编号为1,2,3的3个白色乒乓球,乙盒子中有编号为4,5,6的3个黄色乒乓球,现分别从盒子中随机地取出1个乒乓球,则取出乒乓球的编号之和能被3整除的概率为( )| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{7}{9}$ |
分析 列举出所有情况,看取出乒乓球的编号之和能被3整除的情况占总情况的多少即可.
解答 解:列树状图得:
共有9种情况,编号之和能被3整除的有3种,所以概率是$\frac{1}{3}$.
故选:C.
点评 此题主要考查了利用树状图法求概率,利用如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$是解题关键.

练习册系列答案
相关题目
16.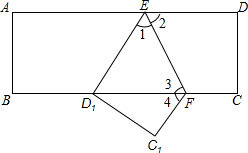 如图,把一个长方形纸片ABCD沿EF折叠后,点D、C分别落在D1、C1位置,其中D1在BC上,则下列结论错误的是( )
如图,把一个长方形纸片ABCD沿EF折叠后,点D、C分别落在D1、C1位置,其中D1在BC上,则下列结论错误的是( )
 如图,把一个长方形纸片ABCD沿EF折叠后,点D、C分别落在D1、C1位置,其中D1在BC上,则下列结论错误的是( )
如图,把一个长方形纸片ABCD沿EF折叠后,点D、C分别落在D1、C1位置,其中D1在BC上,则下列结论错误的是( )| A. | ∠C1=∠C1D1E=90° | B. | ∠1+∠2+∠4=180° | C. | CF=C1F=CD | D. | ∠BD1E=2∠3 |
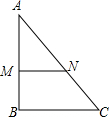 如图,在△ABC中,AC=10,AB=8,直线l分别与AB,AC交于M,N两点,且l∥BC,若S△AMN:S△ABC=4:9,则AM+AN的长为( )
如图,在△ABC中,AC=10,AB=8,直线l分别与AB,AC交于M,N两点,且l∥BC,若S△AMN:S△ABC=4:9,则AM+AN的长为( )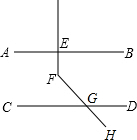 如图,AB∥CD,EF⊥AB,FH交CD于G,若∠EFH=125°,则∠DGH=35°.
如图,AB∥CD,EF⊥AB,FH交CD于G,若∠EFH=125°,则∠DGH=35°.