题目内容
11.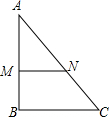 如图,在△ABC中,AC=10,AB=8,直线l分别与AB,AC交于M,N两点,且l∥BC,若S△AMN:S△ABC=4:9,则AM+AN的长为( )
如图,在△ABC中,AC=10,AB=8,直线l分别与AB,AC交于M,N两点,且l∥BC,若S△AMN:S△ABC=4:9,则AM+AN的长为( )| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
分析 由l∥BC,得到△AMN∽△ABC,根据相似三角形的性质即可得到结论.
解答 解:∵l∥BC,
∴△AMN∽△ABC,
∴$\frac{AM}{AB}=\frac{AN}{AC}$,$\frac{{S}_{△AMN}}{{S}_{△ABC}}$=$(\frac{AM}{AN})^{2}$=$\frac{4}{9}$,
∴$\frac{AM}{AB}=\frac{AN}{AC}$=$\frac{2}{3}$,
∴$\frac{AM+AN}{AB+AC}=\frac{2}{3}$,
∵AC=10,AB=8,
∴$\frac{AM+AN}{10+8}=\frac{2}{3}$,
∴AM+AN=12,
故选B.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
6.多项式4x2-4与多项式x2-2x+1的公因式是( )
| A. | x-1 | B. | x+1 | C. | x2-1 | D. | (x-1)2 |
16.计算:($\sqrt{2}$+π)0-2|1-sin30°|+($\frac{1}{2}$)-1=( )
| A. | 2 | B. | -4 | C. | -3 | D. | 1 |
3.下列说法中,不正确的是( )
| A. | 5是25的算术平方根 | B. | m2n与mn2是同类项 | ||
| C. | 多项式-3a3b+7ab+1的次数是4 | D. | -8的立方根为-2 |
1.甲盒子中有编号为1,2,3的3个白色乒乓球,乙盒子中有编号为4,5,6的3个黄色乒乓球,现分别从盒子中随机地取出1个乒乓球,则取出乒乓球的编号之和能被3整除的概率为( )
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{7}{9}$ |
 如图,在平面直角坐标系中,抛物线y=-x2+4x+c与y轴交于点A,过点A作AB∥x轴交抛物线于点B,则以AB为边的等边三角形ABC的周长为12.
如图,在平面直角坐标系中,抛物线y=-x2+4x+c与y轴交于点A,过点A作AB∥x轴交抛物线于点B,则以AB为边的等边三角形ABC的周长为12.