题目内容
4.等腰△ABC中,AB=AC,AD是高,E是AD上的一点,过C点作AB的平行线交BE延长线于F(1)求证:BE2=EG•EF;
(2)当E在AD的延长线上时,其它条件不变,(1)中的结论是否成立?为什么?

分析 (1)根据等腰三角形三线合一的特点推知BE=CE,可通过证△ECG和△EFC相似,根据相似三角形得出的对应成比例线段,由此证得结论;
(2)(1)中的结论仍成立,证明过程同上.
解答  (1)证明:如图1,∵△ABC中,AB=AC,D为BC中点,
(1)证明:如图1,∵△ABC中,AB=AC,D为BC中点,
∴AD是线段BC的垂直平分线,
∴AD平分∠BAC,BE=CE.
∵CF∥AB,
∴∠CFG=∠ABF;
∵∠ABE=∠ACE,
∴∠CFG=∠ACE=∠CFE,
∵∠CEG=∠FEC,
∴△ECG∽△EFC,
∴EC2=EG•EF,
∴BE2=EG•EF;
(2)解:(1)中的结论仍成立,理由如下:
∵△ABC中,AB=AC,D为BC中点,
∴AE是线段BC的垂直平分线,
∴AD平分∠BAC,BE=CE.
∴∠EBC=∠ECD,
∴∠ABE=∠ACE,
∵CF∥AB,
∴∠CFG=∠ABF;
∴∠CFG=∠ACE=∠CFE,
∵∠CEG=∠FEC,
∴△ECG∽△EFC,
∴EC2=EG•EF,
∴BE2=EG•EF.
点评 本题主要考查了等腰三角形的性质、平行线的性质、相似三角形的判定和应用等知识,综合性强,难度较大.

练习册系列答案
相关题目
13.下列不等式一定成立的是( )
| A. | 3-x<4-x | B. | -b>-2b | C. | 4a>3a | D. | $\frac{3}{c}>\frac{2}{c}$ |
14.下列四个式子中,属于代数式的是( )
| A. | x+y=y+x | B. | -a | C. | S=$\frac{1}{2}ah$ | D. | 3x-1>0 |
12. 如图,已知△ABC,∠C=90°,按以下步骤:①分别以A、B为圆心,以大于$\frac{1}{2}AB$的长为半径作弧,两弧相交于两点M、N;②作直线MN交BC于点D.若AC=1.5,∠B=15°.则BD等于( )
如图,已知△ABC,∠C=90°,按以下步骤:①分别以A、B为圆心,以大于$\frac{1}{2}AB$的长为半径作弧,两弧相交于两点M、N;②作直线MN交BC于点D.若AC=1.5,∠B=15°.则BD等于( )
 如图,已知△ABC,∠C=90°,按以下步骤:①分别以A、B为圆心,以大于$\frac{1}{2}AB$的长为半径作弧,两弧相交于两点M、N;②作直线MN交BC于点D.若AC=1.5,∠B=15°.则BD等于( )
如图,已知△ABC,∠C=90°,按以下步骤:①分别以A、B为圆心,以大于$\frac{1}{2}AB$的长为半径作弧,两弧相交于两点M、N;②作直线MN交BC于点D.若AC=1.5,∠B=15°.则BD等于( )| A. | 1.5 | B. | 2 | C. | 2.5 | D. | 3 |
14.已知,函数y=3x的图象经过点A(1,y1),点B(-2,y2),则( )
| A. | y1>y2 | B. | y1<y2 | ||
| C. | y1=y2 | D. | y1、y2无法比较大小 |
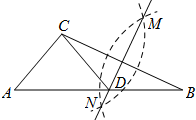 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=25°,则∠ACB的度数为105°.
如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=25°,则∠ACB的度数为105°. (1)如图,若图中小正方形的边长为1,则△ABC的面积为$\frac{7}{2}$.
(1)如图,若图中小正方形的边长为1,则△ABC的面积为$\frac{7}{2}$.