题目内容
已知△ABC中，AB=AC，AD⊥BC于D，△ABC的周长为36cm，△ADC的周长为30cm，那么AD= ．
考点：等腰三角形的性质
专题：
分析：由已知可得，△ABC为等腰三角形，可知D为BC的中点，所以△ABC的周长=△ABD的周长的2倍减去2倍AD的长度即可．代入数据便可得到AD的长度．
解答：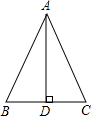
解：根据题意，AB=AC，
∴△ABC为等腰三角形，
∵AD⊥BC，即D为BC的中点，
∵L△ABC=36cm，
L△ADC=30cm，
∴2AD=2L△ADC-L△ABC=24cm，
∴AD=12cm．
故答案为：12cm．
解：根据题意，AB=AC，∴△ABC为等腰三角形，
∵AD⊥BC，即D为BC的中点，
∵L△ABC=36cm，
L△ADC=30cm，
∴2AD=2L△ADC-L△ABC=24cm，
∴AD=12cm．
故答案为：12cm．
点评：本题考查了等腰三角形的性质；观察图形结合已知发现并利用△ABD的周长与△ABC的周长的一半的关系式正确解答本题的关键．做题时要注意观察图形，有时要根据图形上的已知与未知的位置来选择方法．
练习册系列答案
相关题目
如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．
如图，在平面直角坐标系中有两点A（4，0）和B（0，3），则这两点之间的距离为
如图，在四边形ABCD中，对角线AC、BD相交于点O，其中AC+BD=14，CD=5．
如图，将一张长方形纸片沿EF折叠后，点D、C分别落在点D′、C′的位置，ED′的延长线与BC相交于点G，若∠EFG=60°，则∠1=
如图，△ABC中，∠ACB=90°，将△ABC的边BC沿∠ACB的平分线CD折叠到B′C，B′在AC上，若∠DB′A=130°，则∠A=