题目内容
4.点(-1,y1),(1,y2),(4,y3)都在抛物线y=-x2+4x+m上,则y1,y2,y3的大小关系是( )| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y1<y3<y2 |
分析 先求出二次函数的对称轴并确定出抛物线开口向下,然后根据点到对称轴的距离的大小判断即可.
解答 解:∵y=-x2+4x+m=-(x-2)2+4+m,
∴抛物线对称轴为直线x=2,
∵a=-1<0,
∴抛物线开口向下,
且当x<2时,y随x的增大而增大,
当x>2时,y随x的增大而减小,
∵2-(-1)=3,
2-1=1,
4-2=2,
∴y1,y2,y3的大小关系是y1<y3<y2.
故选D.
点评 本题考查了二次函数图象上点的坐标特征,本题利用二次函数的对称性以及增减性求解更简便.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14. 有理数a,b在数轴上的位置如图,那么下列关系正确的是( )
有理数a,b在数轴上的位置如图,那么下列关系正确的是( )
 有理数a,b在数轴上的位置如图,那么下列关系正确的是( )
有理数a,b在数轴上的位置如图,那么下列关系正确的是( )| A. | b>a | B. | -a>b | C. | |a|>|b| | D. | a>-b |
15.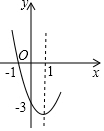 已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )
已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )
 已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )
已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )| A. | -1<x<4 | B. | x<-1或x>3 | C. | x<-1或x>4 | D. | -1<x<3 |
16.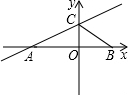 如图,直线y=$\frac{1}{3}$x+1与x轴,y轴分别相交于点A,C两点,点B在x轴上,连结BC,若∠ACB=135°,则点B的坐标为( )
如图,直线y=$\frac{1}{3}$x+1与x轴,y轴分别相交于点A,C两点,点B在x轴上,连结BC,若∠ACB=135°,则点B的坐标为( )
 如图,直线y=$\frac{1}{3}$x+1与x轴,y轴分别相交于点A,C两点,点B在x轴上,连结BC,若∠ACB=135°,则点B的坐标为( )
如图,直线y=$\frac{1}{3}$x+1与x轴,y轴分别相交于点A,C两点,点B在x轴上,连结BC,若∠ACB=135°,则点B的坐标为( )| A. | (1,0) | B. | ($\sqrt{2}$,0) | C. | (2,0) | D. | ($\sqrt{5}$,0) |
13.已知4辆板车和5辆卡车一次共运31吨货,10辆板车和3辆卡车一次能运的货相当,如果设每辆板车每次可运x吨货,每辆卡车每次运y吨货,则可列方程组( )
| A. | $\left\{\begin{array}{l}{10x+5y=31}\\{4x=3y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{4x+5y=31}\\{10x-3y=0}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{4x=5y}\\{10x+3y=31}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{4x+31=5y}\\{10x=3y}\end{array}\right.$ |
14.甲、乙两个搬运工搬运某种货物,已知乙比甲每小时多搬运600kg,甲搬运5000kg所用的时间与乙搬运8000kg所用的时间相等,求甲、乙两人每小时分别搬运多少kg货物.设甲每小时搬运xkg货物,则可列方程为( )
| A. | $\frac{5000}{x-600}$=$\frac{8000}{x}$ | B. | $\frac{5000}{x+600}$=$\frac{8000}{x}$ | C. | $\frac{5000}{x}$=$\frac{8000}{x+600}$ | D. | $\frac{5000}{x}$=$\frac{8000}{x-600}$ |
 如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=2,DB=1,S△ADE=4,则S四边形DBCE( )
如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=2,DB=1,S△ADE=4,则S四边形DBCE( )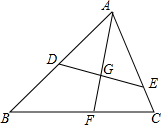 如图,在△ABC中,D、E分别是AB、AC上的点,AE=4,AB=6,AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F.
如图,在△ABC中,D、E分别是AB、AC上的点,AE=4,AB=6,AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F.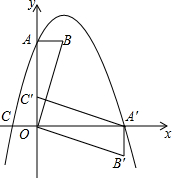 在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.