题目内容
19.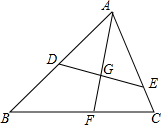 如图,在△ABC中,D、E分别是AB、AC上的点,AE=4,AB=6,AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F.
如图,在△ABC中,D、E分别是AB、AC上的点,AE=4,AB=6,AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F.(1)请你直接写出图中所有的相似三角形;
(2)求AG与GF的比.
分析 (1)可得到三组三角形相似;
(2)先利用两组对应边的比相等且夹角对应相等的两个三角形相似证明△ADE∽△ACB,则∠ADG=∠C,再利用有两组角对应相等的两个三角形相似证明△ADG∽△ACF,然后利用相似比和比例的性质求$\frac{AG}{GF}$的值.
解答 解:(1)△ADG∽△ACF,△AGE∽△AFB,△ADE∽△ACB;
(2)∵$\frac{AE}{AB}$=$\frac{4}{6}$=$\frac{2}{3}$,$\frac{AD}{AC}$=$\frac{2}{3}$,
∴$\frac{AE}{AB}$=$\frac{AD}{AC}$,
又∵∠DAE=∠CAB,
∴△ADE∽△ACB,
∴∠ADG=∠C,
∵AF为角平分线,
∴∠DAG=∠FAE
∴△ADG∽△ACF,
∴$\frac{AG}{AF}$=$\frac{AD}{AC}$=$\frac{2}{3}$,
∴$\frac{AG}{GF}$=2.
点评 本题考查了相似三角形的判断:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9. 有理数a、b在数轴上的位置如图所示,则下列各式正确的是( )
有理数a、b在数轴上的位置如图所示,则下列各式正确的是( )
 有理数a、b在数轴上的位置如图所示,则下列各式正确的是( )
有理数a、b在数轴上的位置如图所示,则下列各式正确的是( )| A. | ab>0 | B. | |b|<|a| | C. | b<0<a | D. | a+b>0 |
7.化简$\frac{1}{a-1}$-$\frac{a}{a-1}$,结果正确的是( )
| A. | -1 | B. | 1 | C. | 0 | D. | ±1 |
4.点(-1,y1),(1,y2),(4,y3)都在抛物线y=-x2+4x+m上,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y1<y3<y2 |
11.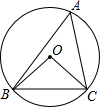 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的大小为( )
如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的大小为( )
 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的大小为( )
如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的大小为( )| A. | 40° | B. | 50° | C. | 80° | D. | 100° |
9. 某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )
某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )
 某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )
某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )| A. | 0.1 | B. | 0.17 | C. | 0.33 | D. | 0.4 |
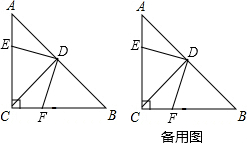 在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E是边AC上的一动点,点F是边BC上的一动点.
在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E是边AC上的一动点,点F是边BC上的一动点. 在直角坐标系中,点C的坐标为(-3,0),将线段OC绕原点O顺时针旋转120°,得到线段OB.
在直角坐标系中,点C的坐标为(-3,0),将线段OC绕原点O顺时针旋转120°,得到线段OB.