Question

如图，写出三角形ABC三个顶点的坐标，并求出三角形ABC的面积．

Answer 1

考点：坐标与图形性质,三角形的面积

专题：计算题

分析：用“割、补”法把三角形ABC的面积转化为S_矩形DEBF-S_△AEB-S_△BCF-S_△ADC，然后根据矩形和三角形的面积公式计算．

解答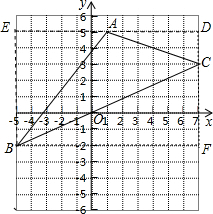：解：如图，
S_△ABC=S_矩形DEBF-S_△AEB-S_△BCF-S_△ADC
=12×7-

1

2

×6×7-

1

2

×12×5-

1

2

×2×6
=27．

点评：本题考查了坐标与图形性质：有图形中一些点的坐标求面积时，过已知点向坐标轴作垂线，然后求出相关的线段长，是解决这类问题的基本方法和规律．
若坐标系内的四边形是非规则四边形，通常用平行于坐标轴的辅助线用“割、补”法去解决问题．