题目内容
17. 如图,点P、Q是边长为2的菱形ABCD中两边BC和CD的中点,K是BD上一动点,则KP+KQ的最小值为2.
如图,点P、Q是边长为2的菱形ABCD中两边BC和CD的中点,K是BD上一动点,则KP+KQ的最小值为2.
分析 先作点P关于BD的对称点P′,连接P′Q交BD于K,此时PK+QK有最小值.然后证明四边形BCQP′为平行四边形,即可求出PK+QK=P′Q=BC=2.
解答  解:作点P关于BD的对称点P′,连接P′Q交BD于K,此时KP+KQ有最小值,最小值为P′Q的长.
解:作点P关于BD的对称点P′,连接P′Q交BD于K,此时KP+KQ有最小值,最小值为P′Q的长.
∵菱形ABCD关于BD对称,P是BC边上的中点,
∴P′是AB的中点,
又∵Q是CD边上的中点,
∴BP′∥CQ,BP′=CQ,
∴四边形BCQP′是平行四边形,
∴P′Q=BC=2,
∴PK+KQ=P′Q=2,即KP+KQ的最小值为2,
故答案为:2.
点评 本题考查的是轴对称-最短路线问题及菱形的性质,熟知两点之间线段最短的知识是解答此题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
7.广东某县生产柚子,其中A村有柚子200吨,B村有柚子280吨,先将这些柚子运到C、D两个仓库.已知C仓库可存储260吨,D仓库可存储220吨,从A村运往C、D两处的费用分别为每吨20元和25元;从B村运往C、D两仓库的费用分别为每吨16元和20元.设从A村运往C仓库的柚子重量为x吨,A、B两村运往两仓库的柚子运输费用分别为yA元,yB元.
(1)请填写下表,并求出yA,yB与x之间的函数关系式.
(2)考虑到B村的经济承受能力,B村的柚子运费不得超过4800元,在这种情况下,请问怎样调运,才能使两村运费之和最小?最小是多少?求出这个最小值.
(1)请填写下表,并求出yA,yB与x之间的函数关系式.
| C | D | 总计 | |
| A | x吨 | 200-x | 200吨 |
| B | 260-x | x+20 | 280吨 |
| 总计 | 260吨 | 220吨 | 480吨 |
12.如图所示的是某几何体的三视图及相关数据,则该几何体的侧面积是( )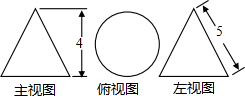

| A. | 30π | B. | 24π | C. | 15π | D. | 12π |
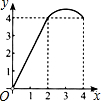
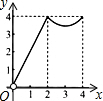
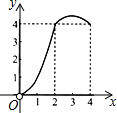
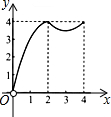
 如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向点B运动,到点B时停止运动;同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同.设点E的运动路程为x,△AEF的面积为y,能大致刻画y与x的函数关系的图象是( )
如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向点B运动,到点B时停止运动;同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同.设点E的运动路程为x,△AEF的面积为y,能大致刻画y与x的函数关系的图象是( )