题目内容
18.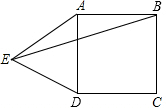 如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB=( )
如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB=( )| A. | 10° | B. | 15° | C. | 30° | D. | 150° |
分析 由于四边形ABCD是正方形,△ADE是正三角形,由此可以得到AB=AE,接着利用正方形和正三角形的内角的性质即可求解.
解答 解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
又∵△ADE是正三角形,
∴AE=AD,∠DAE=60°,
∴△ABE是等腰三角形,∠BAE=90°+60°=150°,
∴∠ABE=∠AEB=15°.
故选:B.
点评 此题主要考查了正方形和等边三角形的性质,同时也利用了三角形的内角和,解题首先利用正方形和等边三角形的性质证明等腰三角形,然后利用等腰三角形的性质即可解决问题.

练习册系列答案
相关题目
9.在△ABC中,已知∠A=∠B=45°,BC=$\sqrt{2}$,则边AB的长为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
13.在下列4种正多边形的瓷砖图案中不能铺满地面的是( )
| A. |  | B. |  | C. |  | D. |  |
10.统计得到一组数据,其中最大值是136,最小值是52,取组距为10,可以分成( )
| A. | 10组 | B. | 9组 | C. | 8组 | D. | 7组 |
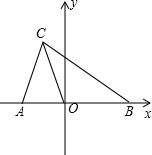 如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,3),且|$\frac{a}{2}$$+\frac{b}{3}$|+(4a-b+11)2=0.
如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,3),且|$\frac{a}{2}$$+\frac{b}{3}$|+(4a-b+11)2=0. 如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1,l2交于点C.
如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1,l2交于点C.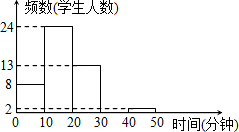 李老师为了了解本班学生作息时间,调查班上50名学生上学路上所花的时间,他发现学生所花时间都少于50min,然后将调查数据整理,作出如图15所示的频数直方图的一部分.
李老师为了了解本班学生作息时间,调查班上50名学生上学路上所花的时间,他发现学生所花时间都少于50min,然后将调查数据整理,作出如图15所示的频数直方图的一部分.