题目内容
已知抛物线y=x2+bx+c的图象经过三点(0,
),(sinA,0),(sinB,0),且A,B为直角三角形的两个锐角,求其解析式.
| 12 |
| 25 |
考点:待定系数法求二次函数解析式
专题:
分析:由点(0,
)可求得c,又因为(sinA,0),(sinB,0)为与x轴的交点,所以可知sinA+sinB=-b,结合条件知-b=1,可求得解析式.
| 12 |
| 25 |
解答:解:∵图象过点(0,
),
∴c=
,
∵图象过点(sinA,0)和(sinB,0),
即函数图象与x轴的交点为(sinA,0)和(sinB,0),
∴方程x2+bx+c=0的两根为sinA和sinB,
由根与系数的关系可知sinA+sinB=-b,
∵A,B为直角三角形的两个锐角,
∴sinA+sinB=1,
∴b=-1,
∴抛物线的解析式为y=x2-x+
.
| 12 |
| 25 |
∴c=
| 12 |
| 25 |
∵图象过点(sinA,0)和(sinB,0),
即函数图象与x轴的交点为(sinA,0)和(sinB,0),
∴方程x2+bx+c=0的两根为sinA和sinB,
由根与系数的关系可知sinA+sinB=-b,
∵A,B为直角三角形的两个锐角,
∴sinA+sinB=1,
∴b=-1,
∴抛物线的解析式为y=x2-x+
| 12 |
| 25 |
点评:本题主要考查待定系数法求二次函数解析式,解题的关键是由条件得到-b=sinA+sinB.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
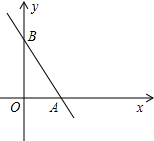 如图,y=kx+b的图象过点P(1,4),且与x轴、y轴的正半轴交于A、B,原点为O,问k、b为何值时,△AOB的面积最小?
如图,y=kx+b的图象过点P(1,4),且与x轴、y轴的正半轴交于A、B,原点为O,问k、b为何值时,△AOB的面积最小?