题目内容
1 2 3 4
8 7 6 5
9 10 11 12
…
若一列数按上述规律排列,则2004在第 行第 列.
8 7 6 5
9 10 11 12
…
若一列数按上述规律排列,则2004在第
考点:规律型:数字的变化类
专题:规律型
分析:观察不难发现,每4个数为一个循环组依次循环,并且第奇数组从左到右排列,第偶数组从右向左排列,用2014除以4,根据商和余数的情况确定答案即可.
解答:解:∵2004÷4=501,
∴2004为第501组的最后一个数,
∴2004在第501行第4列.
故答案为:501;4.
∴2004为第501组的最后一个数,
∴2004在第501行第4列.
故答案为:501;4.
点评:本题是对数字变化规律的考查,观察出每4个数为一个循环组依次循环以及奇数行和偶数行的排列顺序是解题的关键.

练习册系列答案
相关题目
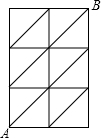 如图,在6个边长为1的小正方形及其部分对角线构成的图形中,如图从A点到B点只能沿图中的线段走,那么从A点到B点的最短距离为( )
如图,在6个边长为1的小正方形及其部分对角线构成的图形中,如图从A点到B点只能沿图中的线段走,那么从A点到B点的最短距离为( )| A、5 | ||
B、2
| ||
C、
| ||
D、
|
 两个正方形如图所示装置,边长分别为m,n,求图阴影部分的面积.
两个正方形如图所示装置,边长分别为m,n,求图阴影部分的面积. 如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发,运动时间为t秒.
如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发,运动时间为t秒.