题目内容
5．
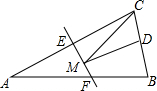如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点，若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为10．
分析 连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AB的垂直平分线可知，点B关于直线EF的对称点为点A，故AD的长为BM+MD的最小值，由此即可得出结论．
解答 
解：连接AD，
∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×4×AD=16，解得AD=8，
∵EF是线段AB的垂直平分线，
∴点B关于直线EF的对称点为点A，
∴AD的长为CM+MD的最小值，
∴△CDM的周长最短=（CM+MD）+CD=AD+$\frac{1}{2}$BC=8+$\frac{1}{2}$×4=8+2=10．
故答案为：10．
点评 本题考查的是轴对称-最短路线问题，熟知等腰三角形三线合一的性质是解答此题的关键．
练习册系列答案
相关题目
13．
如图，以数轴的单位长度线段为边作一个正方形，以表示数-2的点为圆心，正方形对角线长为半径画弧，交数轴于点A，则点A表示的数是（ ）
如图，以数轴的单位长度线段为边作一个正方形，以表示数-2的点为圆心，正方形对角线长为半径画弧，交数轴于点A，则点A表示的数是（ ）| A． | -$\sqrt{2}$ | B． | -2+$\sqrt{2}$ | C． | -2-$\sqrt{2}$ | D． | 1-$\sqrt{2}$ |
20．某城市自来水费实行阶梯水费，收费标准如下表：
（1）某用户十二月份用水30吨，用含a的代数式表示该用户十二月份所交的水费；
（2）若a=1.5元，某用户十二月份交了30元水费，求该用户十二月份的用水量．
| 月用水量 | 不超过12吨的部分 | 超过12吨不超过20吨的部分 | 超过20吨的部分 |
| 收费标准（元/吨） | a | a+1 | 4 |
（2）若a=1.5元，某用户十二月份交了30元水费，求该用户十二月份的用水量．
如图，在平面直角坐标系中，点O是坐标原点，A（0，6），AB=4$\sqrt{3}$，且∠OBA=60°，将△OAB沿直线AB翻折，得到△CAB，点O与点C对应．