题目内容
已知在△ABC中,tan∠B=2,tan∠C=3,BC=5,点D、E分别在边AB、AC上,且DE∥BC,把△ADE沿直线DE翻折,点A落在点P处,若点P到直线BC的距离为2,求DE的长.
考点:翻折变换(折叠问题)
专题:
分析:如图1,若点P在△ABC的内部时,根据题意结合图形求出AQ的长度,进而求出AM的长度,利用相似三角形的性质即可求出DE的长度;如图2,当点P在△ABC的外部时类比前面的解法,同理可求出DE的长度.
解答: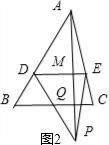
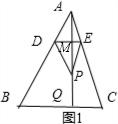 解:如图1,当点P在△ABC的内部时,
解:如图1,当点P在△ABC的内部时,
连接AP并延长交BC于点Q,交DE于点M;
由题意得:AP⊥DE,而DE∥BC,
∴AP⊥BC,即PQ⊥BC,
∴PQ=2;
设BQ=x,CQ=y,则x+y=5;
∵tan∠B=2,tan∠C=3,
∴
=2,
=3,
∴x:y=3:2,
又∵x=y=5,
∴x=3,y=2;
∴AQ=2x=6,AP=6-2=4;
∴AM=
AP=2;
∵DE∥BC,
∴△ADE∽△ABC,
∴
=
,
∴DE=
=
,
即DE的长为
.
如图2,当点P在△ABC的外部时,
连接AP交BC于点Q,AP交DE于点M;
由图1知:
AQ=6,PQ=2,
∴AP=8,AM=
AP=4;
类比以上解法,
同理可求DE=
,
即DE的长为
.

 解:如图1,当点P在△ABC的内部时,
解:如图1,当点P在△ABC的内部时,连接AP并延长交BC于点Q,交DE于点M;
由题意得:AP⊥DE,而DE∥BC,
∴AP⊥BC,即PQ⊥BC,
∴PQ=2;
设BQ=x,CQ=y,则x+y=5;
∵tan∠B=2,tan∠C=3,
∴
| AQ |
| x |
| AQ |
| y |
∴x:y=3:2,
又∵x=y=5,
∴x=3,y=2;
∴AQ=2x=6,AP=6-2=4;
∴AM=
| 1 |
| 2 |
∵DE∥BC,
∴△ADE∽△ABC,
∴
| DE |
| BC |
| AM |
| AQ |
∴DE=
| 2×5 |
| 6 |
| 5 |
| 3 |
即DE的长为
| 5 |
| 3 |
如图2,当点P在△ABC的外部时,
连接AP交BC于点Q,AP交DE于点M;
由图1知:
AQ=6,PQ=2,
∴AP=8,AM=
| 1 |
| 2 |
类比以上解法,
同理可求DE=
| 10 |
| 3 |
即DE的长为
| 10 |
| 3 |
点评:该命题以三角形为载体,以翻折变换为方法,综合考查了直角三角形的边角关系、相似三角形的判定及其性质的应用等几何知识点;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
若(a-2)2+|b-1|=0,则(b-a)2014的值是( )
| A、2014 | B、-2014 |
| C、1 | D、-1 |
下列说法正确的是( )
| A、近似数2.4×104精确到十分位 |
| B、将数60340精确到千位是6.0×104 |
| C、按科学记数法表示的数6.05×105,其原数是60500 |
| D、近似数8.1750是精确到0.001 |
 如图,△ABC中,AB=AC,
如图,△ABC中,AB=AC,
 如图,MA、MB是⊙O的切线,切点分别为A、B,若∠ACB=65°,则∠AMB=
如图,MA、MB是⊙O的切线,切点分别为A、B,若∠ACB=65°,则∠AMB=