题目内容
在数学的学习过程中,我们要不断地归纳,思考和迁移,这样才能提高我们解决问题的能力:
规律发现:
在学完《数轴》这节课后,小明的作业有两道小题,请你帮他把余下的两空完成:

(1)点A表示的数是2,点B表示的数是6,则线段AB的中点C表示的数为 ;
(2)点A表示的数是-5,点B表示的数是7,则线段AB的中点C表示的数为 ;
发现:点A表示的数是a,点B表示的数是b,则线段AB的中点C表示的数为 .
直接运用:
将数轴按如图(1)所示从某一点开始折出一个等边三角形ABC,设点A表示的数为x-3,点B表示的数为2x+1,C表示的数为x-1,则x值为 ,若将△ABC从图中位置向右滚动,则数字2014对应点将与△ABC的顶点 重合.
类比迁移:
如图(2):OB⊥OX,OA⊥OC,∠COX=30°,若射线OA绕O点每秒30°的速度顺时针旋转,射线OB绕O点每秒20°的速度顺时针旋转,射线OC以每秒10°的速度逆时针旋转,三线同时旋转,当一条射线与直线OX重合时,三条射线同时停止运动,问:运动几秒时,其中一条射线是另外两条射线夹角的平分线?
规律发现:
在学完《数轴》这节课后,小明的作业有两道小题,请你帮他把余下的两空完成:

(1)点A表示的数是2,点B表示的数是6,则线段AB的中点C表示的数为
(2)点A表示的数是-5,点B表示的数是7,则线段AB的中点C表示的数为
发现:点A表示的数是a,点B表示的数是b,则线段AB的中点C表示的数为
直接运用:
将数轴按如图(1)所示从某一点开始折出一个等边三角形ABC,设点A表示的数为x-3,点B表示的数为2x+1,C表示的数为x-1,则x值为
类比迁移:
如图(2):OB⊥OX,OA⊥OC,∠COX=30°,若射线OA绕O点每秒30°的速度顺时针旋转,射线OB绕O点每秒20°的速度顺时针旋转,射线OC以每秒10°的速度逆时针旋转,三线同时旋转,当一条射线与直线OX重合时,三条射线同时停止运动,问:运动几秒时,其中一条射线是另外两条射线夹角的平分线?
考点:角的计算,数轴,角平分线的定义
专题:
分析:(1)根据等边三角形ABC,利用边长相等得出x-1-(2x+1)=2x+1-(x-3),求出x即可,再利用数字2014对应的点与-4的距离为:2014+4=2018,得出2018÷3=672…2,C从出发到2014点滚动672周后再滚动两次,即可得出答案;
(2)关键是分析出2秒时OB与OC重合,所以在2秒以前设运动x秒时,OB是OA与OC的角平分线,3秒时OA与OB重合,所以在3秒以前设运动y秒时,OA是OB与OC的角平分线.
(2)关键是分析出2秒时OB与OC重合,所以在2秒以前设运动x秒时,OB是OA与OC的角平分线,3秒时OA与OB重合,所以在3秒以前设运动y秒时,OA是OB与OC的角平分线.
解答:解:(1)∵将数轴按如图所示从某一点开始折出一个等边三角形ABC,设点A表示的数为x-3,点B表示的数为2x+1,点C表示的数为x-1,
∴x-1-(2x+1)=2x+1-(x-3);
∴-2x=6,
解得:x=-3.
故A表示的数为:x-3=-3-3=-6,
点B表示的数为:2x+1=2×(-3)+1=-5,
即等边三角形ABC边长为1,
数字2014对应的点与-4的距离为:2014+4=2018,
∵2018÷3=672…2,C从出发到2014点滚动672周后再滚动两次,
∴数字2014对应的点将与△ABC的顶点B重合.
故答案为:-3,B;
(2)∵OB⊥OX,OA⊥OC,∠COX=30°,
∴∠AOB=30°,
经分析知2秒时OB与OC重合,所以在2秒以前设运动x秒时,OB是OA与OC的角平分线,
30-10x=60-30x
解得x=1.5.
3秒时OA与OB重合,所以在3秒以前设运动y秒时,OA是OB与OC的角平分线,
30y+10y-90=20y+30-30y
解得y=2.4.
4秒时与OA直线OX重合,设3秒后4秒前运动z秒时OB是OA与OC的角平分线,
20x-60+10x=30x-30-20x
解得x=1.5(舍去).
故运动1.5秒或2.4秒时,其中一条射线是另外两条射线夹角的平分线.
∴x-1-(2x+1)=2x+1-(x-3);
∴-2x=6,
解得:x=-3.
故A表示的数为:x-3=-3-3=-6,
点B表示的数为:2x+1=2×(-3)+1=-5,
即等边三角形ABC边长为1,
数字2014对应的点与-4的距离为:2014+4=2018,
∵2018÷3=672…2,C从出发到2014点滚动672周后再滚动两次,
∴数字2014对应的点将与△ABC的顶点B重合.
故答案为:-3,B;
(2)∵OB⊥OX,OA⊥OC,∠COX=30°,
∴∠AOB=30°,
经分析知2秒时OB与OC重合,所以在2秒以前设运动x秒时,OB是OA与OC的角平分线,
30-10x=60-30x
解得x=1.5.
3秒时OA与OB重合,所以在3秒以前设运动y秒时,OA是OB与OC的角平分线,
30y+10y-90=20y+30-30y
解得y=2.4.
4秒时与OA直线OX重合,设3秒后4秒前运动z秒时OB是OA与OC的角平分线,
20x-60+10x=30x-30-20x
解得x=1.5(舍去).
故运动1.5秒或2.4秒时,其中一条射线是另外两条射线夹角的平分线.
点评:此题主要考查了等边三角形的性质,实数与数轴,一元一次方程等知识,本题将数与式的考查有机地融入“图形与几何”中,渗透“数形结合思想”、“方程思想”等,也是一道较优秀的操作活动型问题,难度程度--中.

练习册系列答案
相关题目
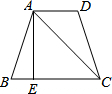 如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点A作AE⊥BC,垂足为点E,∠B=60°,∠CAD=45°,AC=4
如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点A作AE⊥BC,垂足为点E,∠B=60°,∠CAD=45°,AC=4 如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.
如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E. 在△ABC中,D为AB上一点,F为AC上一点,CD与BF交于点E,
在△ABC中,D为AB上一点,F为AC上一点,CD与BF交于点E,