题目内容
3.如图1,△ABC是等边三角形,D是AC边上任意一点,连结DB,以点D为圆心,DB为半径画圆弧,交BC的延长线于E.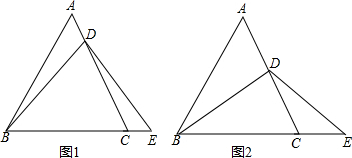
(1)求证:AD=CE;
(2)如图2,若F是BC边任意一点,连结DF,以点D为圆心,DF为半径画圆弧,交BC的延长线于E,请猜想AD、BF、CE之间的数量关系,并证明.
分析 (1)过F作DF∥BC交AB于F,由平行线的性质得到∠AFD=∠ABC,∠ADF=∠ACB,∠FDB=∠DBC,根据已知条件证得AD=DF,由邻补角的定义得到∠BFD=∠DCE=120°,推出△BDF≌△DCE,即可得到结论;
(2)过D 作DG∥AB交BC于G,得到△CDG是等边三角形,推出△DFG≌△DCE,得到FG=CE,等量代换得到结论.
解答  解:(1)过F作DF∥BC交AB于F,
解:(1)过F作DF∥BC交AB于F,
∴∠AFD=∠ABC,∠ADF=∠ACB,∠FDB=∠DBC,
∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB=60°,
∴∠A=∠AFD=∠ADF=60°,
∴AD=DF,
∴∠BFD=∠DCE=120°,
∵BD=ED,
∴∠DBE=∠E,
在△DFB与△DEC中,$\left\{\begin{array}{l}{∠BFD=∠DCE}\\{∠FDB=∠E}\\{BD=DE}\end{array}\right.$,
∴△BDF≌△DCE,
∴DF=CE,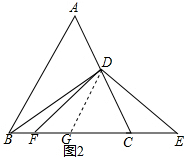
∴AD=CE;
(2)过D 作DG∥AB交BC于G,
∴△CDG是等边三角形,
∴CG=CD,
∵AC=BC,
∴BG=AD,
∴∠DCF=∠DCE=120°,
∵DF=DE,
∴∠DFG=∠E,
在△DFG与△DCE中,$\left\{\begin{array}{l}{∠DFG=∠E}\\{∠DGF=∠DCE}\\{DF=DE}\end{array}\right.$,
∴△DFG≌△DCE,
∴FG=CE,
∵BG=BF+FG,
∴AD=BF+CE.
点评 本题考查了等腰三角形的判定和性质,等边三角形的性质,全等三角形的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目
8.方程2x-x2$-\frac{2}{x}$=0的实根的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
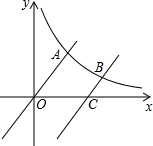 如图,已知函数y=x与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{m}{x}$交于点B,与x轴交于点C,若$\frac{OA}{CB}$=2,则m的值为( )
如图,已知函数y=x与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{m}{x}$交于点B,与x轴交于点C,若$\frac{OA}{CB}$=2,则m的值为( )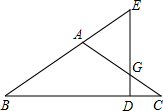 如图,在△ABC中,AB=AC,过AC上的一点G作GD⊥BC于点D,交BA的延长线于点E.
如图,在△ABC中,AB=AC,过AC上的一点G作GD⊥BC于点D,交BA的延长线于点E. 如图所示,C是线段AB上任意一点,M是AC的中点,N是BC的中点,若AB=10cm,求线段MN的长度.
如图所示,C是线段AB上任意一点,M是AC的中点,N是BC的中点,若AB=10cm,求线段MN的长度.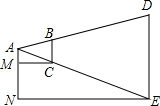 如图所示,某同学拿着一把刻有厘米分划的小尺,站在距旗杆约30m的地方,把手臂向前伸直且让小尺竖直,看到尺上大约有24个分划恰好遮住旗杆.已知此同学的臂长约为60cm,求旗杆的大致高度.
如图所示,某同学拿着一把刻有厘米分划的小尺,站在距旗杆约30m的地方,把手臂向前伸直且让小尺竖直,看到尺上大约有24个分划恰好遮住旗杆.已知此同学的臂长约为60cm,求旗杆的大致高度.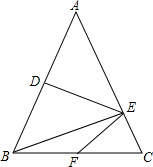 如图,已知在△ABC中,AB=AC,DE垂直平分AB,垂足为点D,连接BE,BE⊥AC.
如图,已知在△ABC中,AB=AC,DE垂直平分AB,垂足为点D,连接BE,BE⊥AC.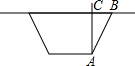 某中学的师生们准备测量一下某段渠水的深度,他们把一根竹竿插到离岸边1m的水底,竹竿高出水面$\frac{1}{3}$m,然后把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,如图所示,则渠水的深度与竹竿的长度分别为$\frac{4}{3}$m,$\frac{5}{3}$m.
某中学的师生们准备测量一下某段渠水的深度,他们把一根竹竿插到离岸边1m的水底,竹竿高出水面$\frac{1}{3}$m,然后把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,如图所示,则渠水的深度与竹竿的长度分别为$\frac{4}{3}$m,$\frac{5}{3}$m.