题目内容
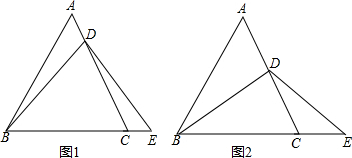
11. 如图,在△ABC中,AB=AC,过AC上的一点G作GD⊥BC于点D,交BA的延长线于点E.
如图,在△ABC中,AB=AC,过AC上的一点G作GD⊥BC于点D,交BA的延长线于点E.(1)AE与AG相等吗?请说明理由;
(2)若∠E=60°,则△AEG是等边三角形吗?请说明理由.
分析 (1)根据等腰三角形的性质可得∠B=∠C,然后根据三角形的外角的性质可以证明∠E=∠DGC=∠AGE,则以及等角对等边即可证得;
(2)根据等边三角形的判定即可得到结论.
解答 解:(1)AE与AG相等,
理由:∵GD⊥BC,
∴∠GDB=∠DGC+∠C=90°,∠EDC=∠B+∠E,
又∵AB=AC,
∴∠B=∠C,
∴∠E=∠DGC=∠AGE,
∴AE=AG;
(2)△AEG是等边三角形,
理由:由(1)证得AE=AG,
∵∠E=60°,
∴△AEG是等边三角形.
点评 本题考查三角形的外角的性质以及等腰三角形的性质以及判定定理,正确理解定理是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.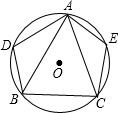 如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )
如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )
 如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )
如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )| A. | 220° | B. | 230° | C. | 240° | D. | 250°° |
6.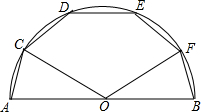 如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )
如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )
 如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )
如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )| A. | 90° | B. | 100° | C. | 108° | D. | 120° |
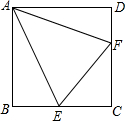 如图所示,在正方形ABCD中,E是CD上的任意一点,以AE为一边作∠EAF=45°,射线AF交BC于F点,连接EF,求证:EF=DE+BF.
如图所示,在正方形ABCD中,E是CD上的任意一点,以AE为一边作∠EAF=45°,射线AF交BC于F点,连接EF,求证:EF=DE+BF.