Question

13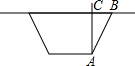．某中学的师生们准备测量一下某段渠水的深度，他们把一根竹竿插到离岸边1m的水底，竹竿高出水面$\frac{1}{3}$m，然后把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，如图所示，则渠水的深度与竹竿的长度分别为$\frac{4}{3}$m，$\frac{5}{3}$m．

Answer 1

分析 根据题意得出各边长，再利用勾股定理得出答案．

解答 解：设竹竿的长度为xm，则AC=（x-$\frac{1}{3}$）=m，
根据题意可得：（x-$\frac{1}{3}$）²+1²=x²，
解得：x=$\frac{5}{3}$，
故渠水的深度为：x-$\frac{1}{3}$=$\frac{5}{3}$-$\frac{1}{3}$=$\frac{4}{3}$（m），
故答案为：$\frac{4}{3}$m，$\frac{5}{3}$m．

点评 此题主要考查了勾股定理的应用，根据题意表示出各边长是解题关键．