题目内容
15.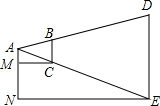 如图所示,某同学拿着一把刻有厘米分划的小尺,站在距旗杆约30m的地方,把手臂向前伸直且让小尺竖直,看到尺上大约有24个分划恰好遮住旗杆.已知此同学的臂长约为60cm,求旗杆的大致高度.
如图所示,某同学拿着一把刻有厘米分划的小尺,站在距旗杆约30m的地方,把手臂向前伸直且让小尺竖直,看到尺上大约有24个分划恰好遮住旗杆.已知此同学的臂长约为60cm,求旗杆的大致高度.[思路引导]
(1)△ABC∽△ADE;
(2)臂长60cm和人距旗杆底部的距离30m分别可看做△ABC和△ADE的对应高,则对应高之比等于BC:DE.
分析 根据平行于三角形一边的直线与其它两边所截得的三角形原三角形相似可判断△ABC∽△ADE;然后根据相似三角形的性质求解.
解答 解:∵BC∥DE,
∴△ABC∽△ADE,
∴$\frac{24}{DE}$=$\frac{60}{30}$
∴DE=12(m),
即旗杆的大致高度为12m.
故答案为△ADE,DE.
点评 本题考查了相似三角形的应用:利用杆或直尺测量物体的高度就是利用杆或直尺的高(长)作为三角形的边,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.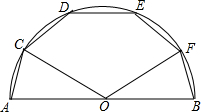 如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )
如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )
 如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )
如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )| A. | 90° | B. | 100° | C. | 108° | D. | 120° |
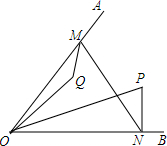 如图,∠AOB=60°,∠POQ=30°,OQ=2,OP=3,点M、N分别在OA、OB上,则PN+MN+QM的最小值为$\sqrt{13}$.
如图,∠AOB=60°,∠POQ=30°,OQ=2,OP=3,点M、N分别在OA、OB上,则PN+MN+QM的最小值为$\sqrt{13}$.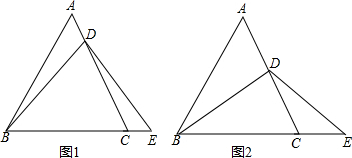
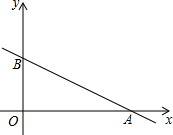 如图所示,一次函数的图象与x轴、y轴分别相交于A,B两点,如果点A的坐标为(4,0),且OA=2OB,试求一次函数的解析式.
如图所示,一次函数的图象与x轴、y轴分别相交于A,B两点,如果点A的坐标为(4,0),且OA=2OB,试求一次函数的解析式.