题目内容
14.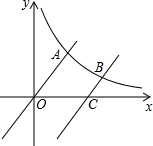 如图,已知函数y=x与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{m}{x}$交于点B,与x轴交于点C,若$\frac{OA}{CB}$=2,则m的值为( )
如图,已知函数y=x与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{m}{x}$交于点B,与x轴交于点C,若$\frac{OA}{CB}$=2,则m的值为( )| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
分析 根据一次函数图象的平移问题由y=x的图象向下平移6个单位得到直线BC的解析式为y=x-6,然后把y=0代入即可确定C点坐标;作AE⊥x轴于E点,BF⊥x轴于F点,易证得Rt△OAE∽△RtCBF,则$\frac{OA}{CB}$=$\frac{AE}{BF}$=2,若设A点坐标为(a,a),则CF=$\frac{1}{2}$a,BF=$\frac{1}{2}$a,得到B点坐标为(6+$\frac{1}{2}$a,$\frac{1}{2}$a),然后根据反比例函数上点的坐标特征得a•a=(6+$\frac{1}{2}$a)•$\frac{1}{2}$a,解得a=4,于是可确定点A的坐标为(4,4),再利用待定系数法确定反比例函数的解析式.
解答 解:∵y=x的图象向下平移6个单位后与与双曲线y=$\frac{m}{x}$交于点B,与x轴交于点C,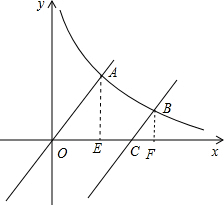
∴直线BC的解析式为y=x-6,
把y=0代入得x-6=0,解得x=6,
∴C点坐标为(6,0);
作AE⊥x轴于E点,BF⊥x轴于F点,如图,
∵OA∥BC,
∴∠AOC=∠BCF,
∴Rt△OAE∽Rt△CBF,
∴$\frac{OA}{BC}$=$\frac{AE}{BF}$=$\frac{OE}{CF}$=2,
设A点坐标为(a,a),则OE=a,AE=a,
∴CF=$\frac{1}{2}$a,BF=$\frac{1}{2}$a,
∴OF=OC+CF=6+$\frac{1}{2}$a,
∴B点坐标为(6+$\frac{1}{2}$a,$\frac{1}{2}$a),
∵点A与点B都在y=$\frac{m}{x}$的图象上,
∴a•a=(6+$\frac{1}{2}$a)•$\frac{1}{2}$a,解得a=4,
∴点A的坐标为(4,4),
把A(4,4)代入y=$\frac{m}{x}$得k=4×4=16,
故选A.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数的解析式.也考查了相似三角形的判定与性质以及一次函数图象的平移问题.

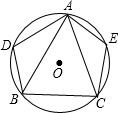 如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )
如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )| A. | 220° | B. | 230° | C. | 240° | D. | 250°° |
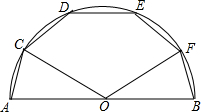 如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )
如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )| A. | 90° | B. | 100° | C. | 108° | D. | 120° |
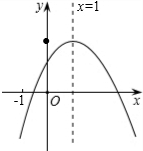 已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断中
已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断中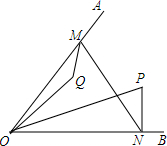 如图,∠AOB=60°,∠POQ=30°,OQ=2,OP=3,点M、N分别在OA、OB上,则PN+MN+QM的最小值为$\sqrt{13}$.
如图,∠AOB=60°,∠POQ=30°,OQ=2,OP=3,点M、N分别在OA、OB上,则PN+MN+QM的最小值为$\sqrt{13}$. 如图所示,观察图形1+3+5+7+9+11=(6)2,由此你能退出从1开始n个连续奇数之和是多少吗?选择几个n的值,用计算器验证一下.
如图所示,观察图形1+3+5+7+9+11=(6)2,由此你能退出从1开始n个连续奇数之和是多少吗?选择几个n的值,用计算器验证一下.