题目内容
18. 如图所示,C是线段AB上任意一点,M是AC的中点,N是BC的中点,若AB=10cm,求线段MN的长度.
如图所示,C是线段AB上任意一点,M是AC的中点,N是BC的中点,若AB=10cm,求线段MN的长度.
分析 由“M为线段AC的中点,N为线段CB的中点”可知AC=2MC,CB=2CN,则有MC+NC=$\frac{1}{2}$(AC+BC);因为AB=AC+BC,MN=MC+NC,即可得解.
解答 解:∵M为线段AC的中点,N为线段CB的中点,
∴AC=2MC,CB=2CN,
∵AB=AC+BC,MN=MC+NC,
∴MN=MC+NC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB=5cm.
故MN的长为5cm.
点评 本题主要考查了两点间的距离,利用中点性质转化线段之间的倍分关系,在不同情况下灵活选用它的不同表示方法,有利于解题的简洁性,此类题还要注意不要漏掉单位.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
8.如果一个数的十位数字是a,个位数字是b,则这个两位数用代数式表示为( )
| A. | ab | B. | ba | C. | 10a+b | D. | 10ab |
6.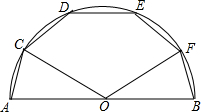 如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )
如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )
 如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )
如图,AB是半圆O的直径,点C、D、E、F在半圆上,AC=CD=DE=EF=FB,则∠COF=( )| A. | 90° | B. | 100° | C. | 108° | D. | 120° |
 如图所示,观察图形1+3+5+7+9+11=(6)2,由此你能退出从1开始n个连续奇数之和是多少吗?选择几个n的值,用计算器验证一下.
如图所示,观察图形1+3+5+7+9+11=(6)2,由此你能退出从1开始n个连续奇数之和是多少吗?选择几个n的值,用计算器验证一下. 随着课程改革的不断深入,对话交流、师生共同探索已成课堂常态,下面的问题取自课堂实录:(在本题计算中sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$,tan37°=$\frac{3}{4}$,cot37°=$\frac{4}{3}$)
随着课程改革的不断深入,对话交流、师生共同探索已成课堂常态,下面的问题取自课堂实录:(在本题计算中sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$,tan37°=$\frac{3}{4}$,cot37°=$\frac{4}{3}$)
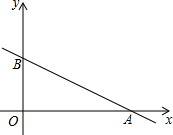 如图所示,一次函数的图象与x轴、y轴分别相交于A,B两点,如果点A的坐标为(4,0),且OA=2OB,试求一次函数的解析式.
如图所示,一次函数的图象与x轴、y轴分别相交于A,B两点,如果点A的坐标为(4,0),且OA=2OB,试求一次函数的解析式.