题目内容
 如图:每个小正方形的边长均为a,连接小正方形的三个顶点得△ABC,则AB边上的高是( )
如图:每个小正方形的边长均为a,连接小正方形的三个顶点得△ABC,则AB边上的高是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:勾股定理,三角形的面积
专题:
分析:求出△ABC的面积,再根据三角形的面积公式即可求得AB边上的高.
解答: 解:S△ABC=S正方形ADEF-S△ADC-S△EBC-S△ABF=4a2-a2-
解:S△ABC=S正方形ADEF-S△ADC-S△EBC-S△ABF=4a2-a2-
a2-a2=
a2,
在Rt△ABF中,AB=
=
a,
∵S△ABC=
AB×h=
a,
∴解得h=
a,即AB边上的高是
a.
故选A.
 解:S△ABC=S正方形ADEF-S△ADC-S△EBC-S△ABF=4a2-a2-
解:S△ABC=S正方形ADEF-S△ADC-S△EBC-S△ABF=4a2-a2-| 1 |
| 2 |
| 3 |
| 2 |
在Rt△ABF中,AB=
| AF2+BF2 |
| 5 |
∵S△ABC=
| 1 |
| 2 |
| 3 |
| 2 |
∴解得h=
3
| ||
| 5 |
3
| ||
| 5 |
故选A.
点评:本题考查的是勾股定理,在解答此题时要进行分类讨论,不要漏解.

练习册系列答案
相关题目
2009年中央预算投入教育和医疗卫生以及社会保障等民生方面的支出达到7285亿元,7285亿元用科学记数法表示为( )
| A、7285×108元 |
| B、72.85×1010元 |
| C、7.285×1011元 |
| D、0.7285×1012元 |
 在四边形ABCD中,AB=CD,M,N分别为BC,AD的中点,延长BA,CD,交MN的延长线分别于点E,F.求证:∠1=∠F.
在四边形ABCD中,AB=CD,M,N分别为BC,AD的中点,延长BA,CD,交MN的延长线分别于点E,F.求证:∠1=∠F.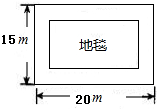 一间会议室,它的地面是长方形的,长为20m,宽为15m,现在准备在会议室地面的中间铺一块地毯,要求四周未铺地毯的部分宽度相等,而且地毯的面积是会议室地面面积的一半,则地面上未铺地毯的部分宽度是多米?
一间会议室,它的地面是长方形的,长为20m,宽为15m,现在准备在会议室地面的中间铺一块地毯,要求四周未铺地毯的部分宽度相等,而且地毯的面积是会议室地面面积的一半,则地面上未铺地毯的部分宽度是多米? 如图,AB、BF分别是⊙O的直径和弦,弦CD与AB、BF分别相交于点E、G,过点F的切线HF与DC的延长线相交于点H,且AB⊥CD.
如图,AB、BF分别是⊙O的直径和弦,弦CD与AB、BF分别相交于点E、G,过点F的切线HF与DC的延长线相交于点H,且AB⊥CD.