题目内容
 如图,矩形ABCD的对角线相交于点O,BE⊥AC于点E,EB的延长线与∠ADC的角平线相交于点F,DF交AC于点M,求证:AC=BF.
如图,矩形ABCD的对角线相交于点O,BE⊥AC于点E,EB的延长线与∠ADC的角平线相交于点F,DF交AC于点M,求证:AC=BF.考点:矩形的性质
专题:
分析:由矩形的性质可得∠COB=2∠CDO,∠EBO=∠BDF+∠F,结合角平分线的定义可求得∠F=∠BDF,可证明BF=BD,结合矩形的性质可得AC=BF.
解答:证明:∵四边形ABCD为矩形,
∴AC=BD,∠ADC=90°,OC=OD,
∴∠COB=2∠CDO,
又∵BE⊥AC,
∴∠COB+∠EBO=90°,
∵∠EBO=∠BDF+∠F,
∴2∠CDO+∠BDF+∠F=90°,
又∵DF平分∠ADC,
∴∠CDO+∠BDF=
∠ADC=45°,
∴2∠CDO+∠BDF+∠F=45°+∠CDO+∠F=90°,
∴∠CDO+∠F=45°,
又∵∠BDF+∠CDO=45°,
∴∠BDF=∠F,
∴BF=BD,
∴AC=BF.
∴AC=BD,∠ADC=90°,OC=OD,
∴∠COB=2∠CDO,
又∵BE⊥AC,
∴∠COB+∠EBO=90°,
∵∠EBO=∠BDF+∠F,
∴2∠CDO+∠BDF+∠F=90°,
又∵DF平分∠ADC,
∴∠CDO+∠BDF=
| 1 |
| 2 |
∴2∠CDO+∠BDF+∠F=45°+∠CDO+∠F=90°,
∴∠CDO+∠F=45°,
又∵∠BDF+∠CDO=45°,
∴∠BDF=∠F,
∴BF=BD,
∴AC=BF.
点评:本题主要考查矩形的性质,掌握矩形的四个角都是直角、对角线互相平分且相等是解题的关键,注意三角形外角性质的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,已知OA=OB,OC=OD,AD、BC相交于点E,则图中全等三角形共有( )
如图所示,已知OA=OB,OC=OD,AD、BC相交于点E,则图中全等三角形共有( )| A、2对 | B、3对 | C、4对 | D、5对 |
 已知一次函数y=kx+b的图象是直线l,根据图象解答下列问题:
已知一次函数y=kx+b的图象是直线l,根据图象解答下列问题: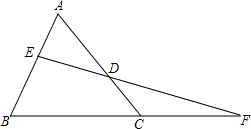 如图,在△ABC(AC>AB)的边AB、AC上分别取点E、D,使BE=CD,连接ED并延长交BC的延长线于点F,判断AB:AC=FD:EF是否成立.
如图,在△ABC(AC>AB)的边AB、AC上分别取点E、D,使BE=CD,连接ED并延长交BC的延长线于点F,判断AB:AC=FD:EF是否成立.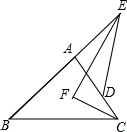 如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC=
如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC= 如图,四边形ACED中,CE∥AD,以DC,DE为边作?DCFE,EC的延长线交AF于B,求证:AB=FB.
如图,四边形ACED中,CE∥AD,以DC,DE为边作?DCFE,EC的延长线交AF于B,求证:AB=FB. 如图,图1中有几对同旁内角?图2,图3,图4呢?观察图形,你能根据上述结论得出其中的规律吗?
如图,图1中有几对同旁内角?图2,图3,图4呢?观察图形,你能根据上述结论得出其中的规律吗? 如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O任作一条直线分别交AB、CD于点E、F.
如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O任作一条直线分别交AB、CD于点E、F.