题目内容
如图，将一副三角尺如图所示叠放在一起，则| AB |
| CD |
考点：解直角三角形
专题：
分析：设AC=k，解Rt△ACB，得出AB=k，解Rt△ACD，得出CD=
k，代入
，计算即可求得答案．
| 3 |
| AB |
| CD |
解答：解：设AC=k．
∵在Rt△ACB中，∠BAC=90°，∠B=45°，
∴AB=AC=k，
∵在Rt△ACD中，∠ACD=90°，∠D=30°，
∴CD=
=
=
k，
∴
=
=
．
故答案为
．
∵在Rt△ACB中，∠BAC=90°，∠B=45°，
∴AB=AC=k，
∵在Rt△ACD中，∠ACD=90°，∠D=30°，
∴CD=
| AC |
| tan30° |
| k | ||||
|
| 3 |
∴
| AB |
| CD |
| k | ||
|
| ||
| 3 |
故答案为
| ||
| 3 |
点评：本题考查了解直角三角形，锐角三角函数的定义，设AC=k，用含k的代数式表示出AB与CD是解题的关键．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
已知两弧长的和l=8π，∠BAC=90°，求半圆形的周长．
如图，数轴上表示1、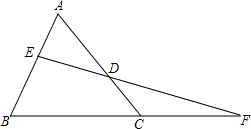
如图，在△ABC（AC＞AB）的边AB、AC上分别取点E、D，使BE=CD，连接ED并延长交BC的延长线于点F，判断AB：AC=FD：EF是否成立．在平面直角坐标系中有一个点A（-
，1），在坐标轴上找一个点P，使得以A、P、O为顶点的三角形是等腰三角形，则这样的点P有（ ）
| 3 |
| A、5个 | B、6个 | C、7个 | D、8个 |
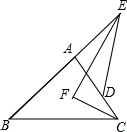如图，△ABC与△ADE有一个公共顶点A，且B，A，E共线，D在边AC上，∠E与∠C的平分线交于点F，若∠B=40°，∠EDA=56°，则∠EFC=
如图，四边形ACED中，CE∥AD，以DC，DE为边作?DCFE，EC的延长线交AF于B，求证：AB=FB．
如图所示，已知OA=OB，OC=OD，AD、BC相交于点E，则图中全等三角形共有（ ）| A、2对 | B、3对 | C、4对 | D、5对 |
已知圆的半径为6cm，圆心到直线l的距离为8cm，那么这条直线和这个圆的公共点的个数是（ ）
| A、0 | B、1 | C、2 | D、无法确定 |