题目内容
 已知等腰△ABC中,AB=AC=13,BC=10,求顶角∠A的正弦值.
已知等腰△ABC中,AB=AC=13,BC=10,求顶角∠A的正弦值.考点:解直角三角形,等腰三角形的性质
专题:
分析:作AD⊥BC于D,CE⊥AB于E,先根据等腰三角形三线合一的性质得出BD=CD=
BC=5,然后在直角三角形ABD中,利用勾股定理求出AD=12,再利用三角形的面积求出CE=
=
.然后在直角三角形ACE中利用锐角三角函数的概念即可求解.
| 1 |
| 2 |
| BC×AD |
| AB |
| 120 |
| 13 |
解答: 解:如图,作AD⊥BC于D,CE⊥AB于E.
解:如图,作AD⊥BC于D,CE⊥AB于E.
∵AD⊥BC,AB=AC,
∴BD=CD=
BC=5.
在直角三角形ABD中,∵∠ADB=90°,AB=13,BD=5,
∴AD=
=12.
∵S△ABC=
×AB×CE=
×BC×AD,
∴CE=
=
=
.
在直角三角形ACE中,∵∠AEC=90°,
∴sin∠CAE=
=
=
.
 解:如图,作AD⊥BC于D,CE⊥AB于E.
解:如图,作AD⊥BC于D,CE⊥AB于E.∵AD⊥BC,AB=AC,
∴BD=CD=
| 1 |
| 2 |
在直角三角形ABD中,∵∠ADB=90°,AB=13,BD=5,
∴AD=
| AB2-BD2 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CE=
| BC×AD |
| AB |
| 10×12 |
| 13 |
| 120 |
| 13 |
在直角三角形ACE中,∵∠AEC=90°,
∴sin∠CAE=
| CE |
| AC |
| ||
| 13 |
| 120 |
| 169 |
点评:本题考查了解直角三角形,等腰三角形的性质,勾股定理,三角形的面积,锐角三角函数的概念,难度适中.通过作高构造包含顶角∠A的直角三角形是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
下列四个图案中,是轴对称图形的个数是( )


| A、1 | B、2 | C、3 | D、4 |
张老师和李老师同时从学校出发,骑车去距学校20千米的县城购买书籍,张老师的汽车速度是李老师的1.5倍,结果张老师比李老师早到40分钟.设张老师骑车速度为x千米/小时,依题意,得到的方程是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
如图,图1,图2,图3分别表示甲乙丙三人由A地到B地的路线图(箭头表示行进的方向),其中E为AB的中点,AH>HB,判断三人行进路线长度的大小关系为( ) 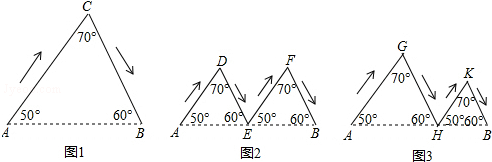

| A、甲<乙<丙 |
| B、甲=乙=丙 |
| C、丙<乙<甲 |
| D、乙<丙<甲 |
 如图,四边形ABCD是菱形,且∠A=60°,又E,F,G,H分别是菱形各边的中点,联结EH,FG,请判断六边形EBFGDH是一个怎样的图形?并说明你的结论.
如图,四边形ABCD是菱形,且∠A=60°,又E,F,G,H分别是菱形各边的中点,联结EH,FG,请判断六边形EBFGDH是一个怎样的图形?并说明你的结论. 如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC=
如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC= 如图,∠AOB和∠COD有公共顶点,OA⊥OC,OB⊥OD,∠AOB:∠COD=7:13,求∠AOB和∠COD的度数.
如图,∠AOB和∠COD有公共顶点,OA⊥OC,OB⊥OD,∠AOB:∠COD=7:13,求∠AOB和∠COD的度数.