题目内容
 如图,落地镜CD直立在地面上,小明在A处看到地面上的物体P的俯角为30°,看到该物体在落地镜CD中像Q的俯角为15°,小明眼睛的高度为1.6m,A,P,C在同一水平面上,若物体高度不计,问物体P离小明有多远?离落地镜有多远?(tan15°=2-
如图,落地镜CD直立在地面上,小明在A处看到地面上的物体P的俯角为30°,看到该物体在落地镜CD中像Q的俯角为15°,小明眼睛的高度为1.6m,A,P,C在同一水平面上,若物体高度不计,问物体P离小明有多远?离落地镜有多远?(tan15°=2-| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:过点P作PM⊥BQ于点M,过点Q作QN∥AC,根据∠BPA=30°,AB=1.6,得出物体P离小明有多远,再根据∠DBP=30°,∠DBQ=15°,得出tan∠MBP=
,设BM=x,则PM=(2-
)x,根据勾股定理求出x的值,从而求出PQ的值,即可得出离落地镜有多远.
| PM |
| BM |
| 3 |
解答: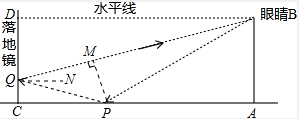 解:过点P作PM⊥BQ于点M,过点Q作QN∥AC,
解:过点P作PM⊥BQ于点M,过点Q作QN∥AC,
∵∠BPA=30°,AB=1.6,
∴PB=3.2m,
∵∠DBP=30°,∠DBQ=15°,
∴∠MBP=15°,∠BQN=15°,
∴tan∠MBP=
=2-
,∠MQP=30°,
∴PQ=2PM,
设BM=x,则PM=(2-
)x,
∴[(2-
)x]2+x2=3.22,
∴x1=
,x2=-
(舍去),
∴PM=
×(2-
)=
,
∴PQ=2×
=
(m);
答:物体P离小明有3.2m,离落地镜有
m远.
 解:过点P作PM⊥BQ于点M,过点Q作QN∥AC,
解:过点P作PM⊥BQ于点M,过点Q作QN∥AC,∵∠BPA=30°,AB=1.6,
∴PB=3.2m,
∵∠DBP=30°,∠DBQ=15°,
∴∠MBP=15°,∠BQN=15°,
∴tan∠MBP=
| PM |
| BM |
| 3 |
∴PQ=2PM,
设BM=x,则PM=(2-
| 3 |
∴[(2-
| 3 |
∴x1=
16+16
| ||
| 15 |
16+16
| ||
| 15 |
∴PM=
16+16
| ||
| 15 |
| 3 |
16
| ||
| 15 |
∴PQ=2×
16
| ||
| 15 |
32
| ||
| 15 |
答:物体P离小明有3.2m,离落地镜有
32
| ||
| 15 |
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
已知圆的半径为6cm,圆心到直线l的距离为8cm,那么这条直线和这个圆的公共点的个数是( )
| A、0 | B、1 | C、2 | D、无法确定 |
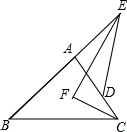 如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC=
如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC= 如图,图1中有几对同旁内角?图2,图3,图4呢?观察图形,你能根据上述结论得出其中的规律吗?
如图,图1中有几对同旁内角?图2,图3,图4呢?观察图形,你能根据上述结论得出其中的规律吗? 如图,两双曲线y=
如图,两双曲线y=
 如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O任作一条直线分别交AB、CD于点E、F.
如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O任作一条直线分别交AB、CD于点E、F. “五•一”节,某超市开展“有奖促销”活动,凡购物不少于30元的顾客均有一次转动转盘的机会(如图,转盘被分为8个全等的小扇形),当指针最终指向数字8时,该顾客获一等奖;当指针最终指向3或5时,该顾客获二等奖(若指针指向分界线则重转). 经统计,当天发放一、二等奖奖品共600份,那么据此估计参与此次活动的顾客为
“五•一”节,某超市开展“有奖促销”活动,凡购物不少于30元的顾客均有一次转动转盘的机会(如图,转盘被分为8个全等的小扇形),当指针最终指向数字8时,该顾客获一等奖;当指针最终指向3或5时,该顾客获二等奖(若指针指向分界线则重转). 经统计,当天发放一、二等奖奖品共600份,那么据此估计参与此次活动的顾客为 如图,AE∥BF,试确定∠ACB与∠EAC和∠FBC的关系(度数不用).
如图,AE∥BF,试确定∠ACB与∠EAC和∠FBC的关系(度数不用).