题目内容
 甲,乙两人在直线跑道上同起点,同终点,同方向匀速跑步500m,先到终点的人原地休息,已知甲先出发2秒,在在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,
甲,乙两人在直线跑道上同起点,同终点,同方向匀速跑步500m,先到终点的人原地休息,已知甲先出发2秒,在在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,(1)求a,b,c的值
(2)画出甲乙两人的距离y(米)与甲出发的时间t(秒)之间关系的草图.(标出相关的数据)
考点:一次函数的应用
专题:
分析:(1)由函数图象可以分别求出甲的速度为1米/秒,乙的速度为5米/秒,就可以求出乙追上甲的时间a的值,b表示甲跑完全程时甲、乙之间的距离,c表示乙出发后多少时间,甲走完全程就用甲走完全程的时间-2就可以得出结论.
(2)根据题意由描点法直接画出图象即可.
(2)根据题意由描点法直接画出图象即可.
解答:解:由题意及函数图象可以得出:
甲的速度为:8÷2=4(米/秒),
乙的速度为:500÷100=5(米/秒),
a=8÷(5-4)=8(秒);
b=500-4×102=92(米),
c=500÷4-2=123(秒).
答:a=8米,b=92米,c=123秒;
(2)由题意,画出图象,得

甲的速度为:8÷2=4(米/秒),
乙的速度为:500÷100=5(米/秒),
a=8÷(5-4)=8(秒);
b=500-4×102=92(米),
c=500÷4-2=123(秒).
答:a=8米,b=92米,c=123秒;
(2)由题意,画出图象,得

点评:本题考查了行程问题的数量关系的运用,一次函数的运用,描点法画函数图象的运用.解答时理解图象标注的数据的含义是关键.

练习册系列答案
相关题目
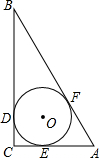 如图,在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm.
如图,在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm. 某小区有100个停车位,给业主停车带来了方便,去年1-6月,每个车位租价y为360元,7-12月,每个车位租价y(元)与月份x关系如表所示.去年1-12月,每月租出车位m(个)与月份x关系如图.已知业主只需支付月租给物管公司,公司每月每车位需支付管理费p=6x(1≤x≤12,x取整数).
某小区有100个停车位,给业主停车带来了方便,去年1-6月,每个车位租价y为360元,7-12月,每个车位租价y(元)与月份x关系如表所示.去年1-12月,每月租出车位m(个)与月份x关系如图.已知业主只需支付月租给物管公司,公司每月每车位需支付管理费p=6x(1≤x≤12,x取整数). 如图,在△ABC中,AD为BC边上的中线,AE:ED=1:2,连结BE并延长交AC于点F.若AF=4,求CF的长.
如图,在△ABC中,AD为BC边上的中线,AE:ED=1:2,连结BE并延长交AC于点F.若AF=4,求CF的长. 已知:如图,在?ABCD中,AE平分∠BAD,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.
已知:如图,在?ABCD中,AE平分∠BAD,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.