题目内容
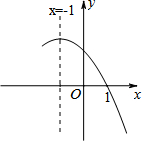如图，下面是二次函数y=ax2+bx+c图象的一部分，则下列结论中，正确的个数是（ ）①2（a+1）＞2
②4a-2b+c＞0
③方程ax2+bx+c=0有两个不等的实数根
④9a-3b+c=0．
| A、1 | B、2 | C、3 | D、4 |
考点：二次函数图象与系数的关系
专题：
分析：根据图象得出开口方向，即可判断①，求出函数和x轴的另一个交点坐标，把x=-2，x=-3分别代入，即可判断②③④．
解答：解：∵二次函数的图象的开口向下，
∴a＜0，
∴2a＜0，
∴2a+2＜2，
即2（a+1）＜2，∴①错误；
∵二次函数的对称轴是直线x=-1，和x轴一个交点是（1，0），则当x=-2时，y＞0，
把x=-2代入y=ax2+bx+c得：y=4a-2b+c＞0，∴②正确；
∵函数和x轴有两个交点，
∴方程ax2+bx+c=0有两个不等的实数根，∴③正确；
∵二次函数的对称轴是直线x=-1，和x轴一个交点是（1，0），
∴另一个交点坐标是（-3，0），
把x=-3代入y=ax2+bx+c得：y=9a-3b+c=0，∴④正确；
故选C．
∴a＜0，
∴2a＜0，
∴2a+2＜2，
即2（a+1）＜2，∴①错误；
∵二次函数的对称轴是直线x=-1，和x轴一个交点是（1，0），则当x=-2时，y＞0，
把x=-2代入y=ax2+bx+c得：y=4a-2b+c＞0，∴②正确；
∵函数和x轴有两个交点，
∴方程ax2+bx+c=0有两个不等的实数根，∴③正确；
∵二次函数的对称轴是直线x=-1，和x轴一个交点是（1，0），
∴另一个交点坐标是（-3，0），
把x=-3代入y=ax2+bx+c得：y=9a-3b+c=0，∴④正确；
故选C．
点评：本题考查了二次函数和x轴的交点问题，函数的对称轴，函数的开口方向等知识点的应用，主要考查学生的观察图象的能力和理解能力，题目比较好，难度适中．
练习册系列答案
阅读快车系列答案
相关题目
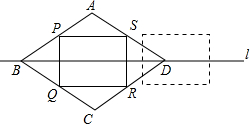在菱形ABCD中，AB=5cm，BD=8cm，P，Q，R，S分别是菱形各边的中点．将长方形PQRS沿着直线L向右移动5cm，则长方形PQRS与菱形ABCD重叠的面积是多少？
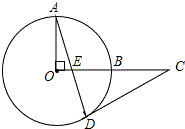如图，OA、OB是⊙O的半径，OA⊥OB，点C是OB延长线上一点，过点C作⊙O的切线，点D是切点，连接AD交OB于点E．求证：CD=CE．