题目内容
13．
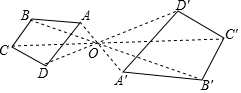如图，四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形，若OA：OA′=2：3，则四边形ABCD与四边形A′B′C′D′的面积比为（ ）| A． | 4：9 | B． | 2：5 | C． | 2：3 | D． | $\sqrt{2}$：$\sqrt{3}$ |
分析 根据题意求出两个相似多边形的相似比，根据相似多边形的性质解答．
解答 解：∵四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形，OA：OA′=2：3，
∴DA：D′A′=OA：OA′=2：3，
∴四边形ABCD与四边形A′B′C′D′的面积比为：（$\frac{2}{3}$）2=$\frac{4}{9}$，
故选：A．
点评 本题考查的是位似变换的性质，掌握位似图形与相似图形的关系、相似多边形的性质是解题的关键．
练习册系列答案
相关题目
2016年11月1日至6日，第十一届中国航展在广东珠海举行．在本次航展上，一架飞机飞行到A点时，测得观礼台C在飞机前下方，俯角为65°，此时飞机飞行路线改为沿坡脚30°的方向朝斜上方直线飞行，飞机飞行6km到达B处，此时飞机飞行高度为5km，另一个观礼台D恰好在飞机的正下方，求两个观礼台C与D之间的距离．
4．
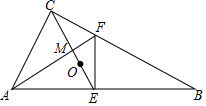如图，直角△ABC中，∠B=30°，点O是△ABC的重心，连接CO并延长交AB于点E，过点E作EF⊥AB交BC于点F，连接AF交CE于点M，则$\frac{MO}{MF}$的值为（ ）
如图，直角△ABC中，∠B=30°，点O是△ABC的重心，连接CO并延长交AB于点E，过点E作EF⊥AB交BC于点F，连接AF交CE于点M，则$\frac{MO}{MF}$的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{5}}{4}$ | C． | $\frac{2}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
1．在最近很火的节目《中国诗词大会》中，除才女武亦姝实力超群之外，其他选手的实力也不容小觑．以下是随机抽取的10名挑战者答对的题目数量的统计：这10名挑战者答对题目数量的中位数和众数分别是5，5．
| 人数 | 3 | 4 | 2 | 1 |
| 答对题数 | 4 | 5 | 7 | 8 |
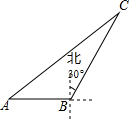如图，海中一渔船在A处且与小岛C相距70nmile，若该渔船由西向东航行30nmile到达B处，此时测得小岛C位于B的北偏东30°方向上；求该渔船此时与小岛C之间的距离．
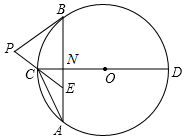如图，在⊙O中，直径CD垂直于不过圆心O的弦AB，垂足为点N，连接AC，点E在AB上，且AE=CE
2．截至2016年底，国家开发银行对“一带一路”沿线国家累计发放贷款超过1600亿美元，其中1600亿用科学记数法表示为（ ）
| A． | 16×1010 | B． | 1.6×1010 | C． | 1.6×1011 | D． | 0.16×1012 |