题目内容
8.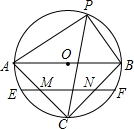 如图,⊙O的直径AB=8,P是圆上任一点(A,B除外),∠APB的平分线交⊙O于C,弦EF过AC,BC的中点M,N,则EF的长是4$\sqrt{3}$.
如图,⊙O的直径AB=8,P是圆上任一点(A,B除外),∠APB的平分线交⊙O于C,弦EF过AC,BC的中点M,N,则EF的长是4$\sqrt{3}$.
分析 由于PC平分∠APB,易得$\widehat{AC}=\widehat{BC}$,如果连接OC交EF于D,根据垂径定理可知:OC必垂直平分EF.由于M、N是AC、BC的中点,因此MN是△ABC的中位线,根据平行线分线段成比例定理可得:OD=CD=$\frac{1}{2}$OC=2.连接OE,可在Rt△OED中求出ED的长,即可得出EF的值.
解答 解:∵PC是∠APB的角平分线,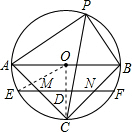
∴∠APC=∠CPB,
∴弧AC=弧BC;
∴AC=BC;
∵AB是直径,
∴∠ACB=90°.
即△ABC是等腰直角三角形.
连接OC,交EF于点D,则OC⊥AB;
∵M、N是AC、BC的中点,
∴MN∥AB;
∴OC⊥EF,OD=$\frac{1}{2}$OC=2.
连接OE,
根据勾股定理,得:
DE=2$\sqrt{3}$,EF=2ED=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 此题综合运用了圆周角定理及其推论发现等腰直角三角形,再进一步根据等腰三角形的性质以及中位线定理,求得EF的弦心距,最后结合垂径定理和勾股定理求得弦长.

练习册系列答案
相关题目
18.在△ABC中,若sinB=$\frac{\sqrt{3}}{2}$,cosA=$\frac{1}{2}$,则△ABC是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |

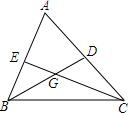 如图,在△ABC中,点G是△ABC的重心,BG和CG延长线分别交AC和AB于点D和E,则$\frac{GC}{CE}$的值为$\frac{2}{3}$.
如图,在△ABC中,点G是△ABC的重心,BG和CG延长线分别交AC和AB于点D和E,则$\frac{GC}{CE}$的值为$\frac{2}{3}$.