题目内容
19.(1)填空:x2+2x+2=(x+1)2+1(2)当x=-1时,x2+2x+2有最小值,最小值是1.
(3)已知x2+y2-2x+6y+10=0,求(x+y)-3的值.
分析 (1)利用配方法解答;
(2)根据非负数的性质解答;
(3)利用平方法把原式变形,根据非负数的性质解答即可.
解答 解:(1)x2+2x+2=x2+2x+1+1=(x+1)2+1;
故答案为:x+1;
(2)当x=-1时,x2+2x+2有最小值,最小值是-1;
故答案为:-1;1.
(3)∵x2+y2-2x+6y+10=0,
∴x2-2x+1+y2+6y+9=0,
则(x-1)2+(y+3)2=0,
∴x-1=0,y+3=0,
解得,x=1,y=-3,
则(x+y)-3=-$\frac{1}{8}$.
点评 本题考查的是配方法的应用,掌握配方法的一般步骤是解题的关键.

练习册系列答案
相关题目
14.三角形的三条边长分别为a,b,c,满足等式(a+b)2-c2=2ab,则此三角形是( )
| A. | 锐角三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 钝角三角形 |
11.计算-1+2-3+4-5+6…-97+98-99的结果为( )
| A. | -50 | B. | -49 | C. | 49 | D. | 50 |
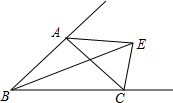 如图,AE,CE分别为△ABC两个外角的角平分线,连结BE,求证:BE平分∠ABC.
如图,AE,CE分别为△ABC两个外角的角平分线,连结BE,求证:BE平分∠ABC.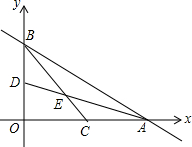 如图,直线y=-$\frac{1}{2}$x+2交x轴于A点,交y轴于B点,C、D分别为OA、OB的中点,连接AD、BC相交于E点.
如图,直线y=-$\frac{1}{2}$x+2交x轴于A点,交y轴于B点,C、D分别为OA、OB的中点,连接AD、BC相交于E点.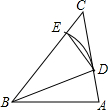 如图,已知△ABC中,∠ABC=∠ACB,以点B为圆心,AB长为半径的弧分别交AC,BC于点D,连接BD,ED,若∠CED=105°,求∠ABC的度数为( )
如图,已知△ABC中,∠ABC=∠ACB,以点B为圆心,AB长为半径的弧分别交AC,BC于点D,连接BD,ED,若∠CED=105°,求∠ABC的度数为( )