题目内容
8.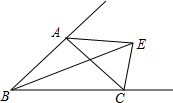 如图,AE,CE分别为△ABC两个外角的角平分线,连结BE,求证:BE平分∠ABC.
如图,AE,CE分别为△ABC两个外角的角平分线,连结BE,求证:BE平分∠ABC.
分析 作EF⊥BA于F,EG⊥AC于G,EH⊥BC于H,根据角平分线的性质定理得到EF=EG,EG=EH,得到EF=EH,根据角平分线的判定定理证明即可.
解答 证明: 作EF⊥BA于F,EG⊥AC于G,EH⊥BC于H,
作EF⊥BA于F,EG⊥AC于G,EH⊥BC于H,
∵AE,CE分别为△ABC两个外角的角平分线,EF⊥BA于F,EG⊥AC于G,EH⊥BC于H,
∴EF=EG,EG=EH,
∴EF=EH,又EF⊥BA,EH⊥BC,
∴BE平分∠ABC.
点评 本题考查的是角平分线的性质和判定,掌握角平分线的性质定理和判定定理是解题的关键.

练习册系列答案
相关题目
18.一元二次方程x2=4x的解是( )
| A. | x=0 | B. | x=4 | C. | x=0或x=4 | D. | x=2或x=-2 |

 一块长16m,宽12m的矩形荒地上,要建一个花园,使花园所占面积为荒地面积的一半,小明的设计方案如图,设花园宽度为xm,欲求x,可列方程(16-x)(12-x)=$\frac{1}{2}$×16×12.
一块长16m,宽12m的矩形荒地上,要建一个花园,使花园所占面积为荒地面积的一半,小明的设计方案如图,设花园宽度为xm,欲求x,可列方程(16-x)(12-x)=$\frac{1}{2}$×16×12.